Memoria

 

Tengo una pantalla en blanco que ‘me observa’. Tengo una idea que quiero desarrollar, pero no sé en qué dirección voy a ir. Me produce un poco de vértigo, porque tiene un componente que no quiero ignorar. Me voy a meter en un terreno en donde hace mucho tiempo me propuse (explícitamente) no entrar. Y voy a violar un pacto conmigo mismo, y por lo tanto, tengo miedo de lo que salga.

En realidad, como no hay nadie que esté mirando lo que escribo, como los pactos (o acuerdos) fueron únicamente conmigo mismo, no voy a ‘fallarle’ a nadie; en todo caso, me fallo a mí. Pero no quiero que ser tozudo o cabeza dura y no advertir que quizás, si no lo hago, me voy a perder una oportunidad de aprender algo. Y no quiero.

Me explico.

En general, todo lo que tiene que ver con la matemática que se enseña (o ha enseñado) en los colegios/escuelas a lo largo de los años, contiene un componente de memorización. Es decir, se trate de las tablas de multiplicar, o las fórmulas más conocidas (para resolver ecuaciones de segundo grado), o el cuadrado de la suma, la diferencia de cuadrados, memorizaciones de varios teoremas (Pitágoras por ejemplo), en alguna parte aparece un componente que es la memoria. Y es allí en donde mis puertas se han cerrado históricamente: ¡no quiero participar de nada que tenga que ver con algún detalle, aunque sea mínimo, que requiera de la utilización de la memoria!

Sin embargo, hace unos días estuve escuchando una charla de un matemático británico y muy joven, Adam Kucharski. Ya había leído su libro (o al menos uno de sus libros) The Perfect Bet, algo así como La apuesta perfecta. El libro es fascinante y contiene maravillosos ejemplos de la vida cotidiana donde el azar empieza a tener cada vez menos incidencia en las decisiones que tomamos. Es decir, si uno no tuviera ni conociera la teoría de probabilidades y estadística, si uno no supiera nada, entonces todo terminaría siendo una sorpresa. Por ejemplo, un caso muy concreto (y muy sencillo) sería el siguiente: si no supiéramos que al tirar una moneda al aire, la probabilidad de que salga cara (o ceca) es de ½, o de un 50% si usted prefiere, entones, decía, cada vez que arrojáramos repetidamente una moneda al aire, su resultado sería inesperado para nosotros: podrían aparecer múltiples caras seguidas, o uno podría sospechar que deberían salir o cualquier otra variante que se le ocurra. Sin embargo, en alguna parte está tan embebida en nuestra cultura (ahora), que en el ‘largo aliento’, si uno tirara una moneda mil veces o cien mil veces, la expectativa sería que se distribuyera por mitades, aproximadamente. Es decir, conocer que la probabilidad es ½ coopera con la expectativa que tenemos.

Al mismo tiempo, lo mismo podríamos decir respecto de un dado o para dar un paso un poquito más sofisticado, si estuviéramos jugando a la ruleta. La moraleja de todo esto es más o menos inmediata: “La ciencia está cooperando para que el factor ‘suerte’ tenga menos incidencia en NUESTRA expectativa”.

Por supuesto, no aspiro a convencerla/o de que la suerte ha desaparecido o desaparecerá. ¡Obviamente, no! Más aún, el azar jugará siempre un lugar central en todos los juegos (de este tipo), pero la ciencia, educa… y de hecho, ese es un tema ciertamente no menor.

Con el avance de las bases de datos, la memoria que uno puede almacenar, permite tener expectativas respecto de lo que uno puede suponer que pasará en algunos juegos que ya no sean esencialmente derivados del azar. Por ejemplo, incluso jugando al ajedrez, en donde uno supone que el azar tiene una incidencia mucho menor, o analizando los comportamientos de diferentes jugadores en un partido de basketball o de tennis, por poner otras alternativas, o al patear penales en partidos de fútbol… todos estos casos ahora tienen un factor extra que no existía hasta hace no mucho tiempo.

Escribí todo esto, pero aún no logré abordar el tema que me interesa: ¡la memoria! Y confieso que no sé, a esta altura, si lo que voy a escribir se compadece con lo que escribí hasta acá. O sea, querría advertirle que aún leyendo el texto que continúa, usted pueda terminar asociando lo que figura más arriba con lo que va a figurar más abajo: ¡no sé! Pero no voy a forzar una ligazón entre ambos, sino que estoy compartiendo con usted lo que me está pasando a mí… en tiempo real, “mientras me está sucediendo”.

En una conferencia que Kucharski dio el primer día de junio del año 2016, promocionada a las 7 de la tarde, en Londres, puso en el pizarrón el siguiente número:

610260100091

Después le pidió a la audiencia que se fijara en el número (que aparecía muy grande en una pantalla) y les dio un minuto para que lo pudieran registrar… como dijo él… de alguna forma.

Yo también quise hacerlo, pero no tuve demasiada suerte. Kucharski, después de quitarlo de la pantalla, preguntó si había algún voluntario. Varios se ofrecieron. Eligió uno y le pidió que lo repitiera. El joven que se había ofrecido repitió el número, pero se equivocó sobre el final, y en lugar de un 9 dijo 8 como penúltimo número. Yo, que había estado atento, sabía que no había ningún 8, pero no recordaba nada más que eso.

Kucharski preguntó si había otra persona que quisiera intentarlo, y así fue como ‘alguien’ dijo el número correctamente. Pero lo notable es que no fue diciendo los dígitos uno por uno, sino que los mencionó así:

610   260  100  091.

Es decir, los reprodujo en grupos de tres. Por supuesto, era el número correcto y la metodología que había usado el joven parecía muy atractiva (y eficiente).

Allí fue donde Kucharski agregó algo que me pareció muy interesante y que es —parte— de lo que quisiera compartir con usted: “Los estudios hechos a los efectos de ‘medir’ cuántos dígitos puede reproducir de memoria una persona promedio, se aproximan a los siete. Es decir, una persona ‘común’, como usted o yo, debería poder en un plazo razonable (menos de un minuto, para encuadrarlo como hizo él), reproducir un número compuesto por siete números. Lo que no dijo, es que esos números que una persona puede reproducir, está compuesto únicamente de siete dígitos. En todo caso, uno puede reproducir siete ‘números’ más pequeños, o siete ‘unidades’. De hecho, lo que nos permite (a los humanos) es recordar/reproducir, los números de teléfono, que en general, en la mayor parte del mundo (al menos en las ciudades más grandes o más pobladas), los números telefónicos están compuestos por siete dígitos.

Inmediatamente, ofreció un ejemplo muy característico y muy interesante: en Francia, los números de teléfono vienen separados… ¡de a pares! (Le propongo que usted verifique este dato por su cuenta porque resulta muy llamativo, y de hecho, me permitió contestar una pregunta que me había hecho hace un tiempo): ¿por qué habrían de presentarse los números en las tarjetas de los restaurantes, o de los hoteles, o en las publicidades en las calles o en las estaciones de trenes, o las líneas aéreas… por mencionar solo algunas, decía, ¿por qué aparecen separados en pares de dígitos?

 

 

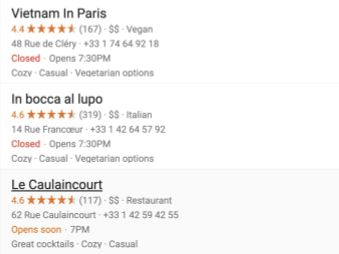
Como usted puede advertir más arriba, elegí en forma aleatoria números de teléfonos de restaurantes (tres) y de líneas aéreas (sin particular orden de preferencia) para mostrar que los franceses, interpretando perfectamente lo que decía Kucharski, ofrecen los números divididos de a pares de manera tal de facilitarle a una persona la posibilidad de recordarlo.

Más allá de seguir con más ejemplos de lo mismo, quiero volver por un instante al número original que había aparecido en la pantalla:

610260100091.

Kucharski hizo una afirmación, que en su momento me pareció atrevida: “Verán que este número en particular ustedes lo van a recordar sin ninguna duda más tarde cuando lleguen a sus casas o donde quiera que vayan hoy por la noche”. ¿Por qué?

Fíjese en lo siguiente: de vuelta el número y en lugar de leerlo de izquierda hacia la derecha, léalo de derecha a izquierda. Lo voy a escribir:

190001062016

Lo voy a dividir en diferentes unidades o trozos:

1900    0106    2016

Ahora, aunque no haga particular necesidad, voy a agregar algunos signos de puntuación:

19:00    01/06    2016

¿Le sugiere algo esta forma de escribir o describir el número?

Es muy posible que usted pueda detectar un patrón: ¡es la hora, día y fecha de la charla a la que estaban concurriendo! Es decir, las 19 horas (las 7 de la tarde), del primer día de junio del año 2016. ¡Y eso es todo!

Antes de avanzar, me imagino su cara… como si me estuviera diciendo: ¿en serio? ¿Cómo se me habría de ocurrir utilizar todo este procedimiento, desde invertir el orden de la lectura, separarlo en diferentes ‘unidades’, agregarles diferentes signos de puntuación… y encima, que éstas coincidan justamente con el horario, día y fecha de la conferencia? Me apresuro a decirle: ¡tendría razón! Yo diría lo mismo y me hubiera pasado lo mismo.

Pero lo que SÍ puedo agregar a esa frase, es que me ha dado (y quizás a usted también), la posibilidad de incorporar algún tipo de estrategia si es que uno quisiera o tuviera que recordar algo.

Un par de agregados más. Creo que fue Eduardo Dubuc (otro matemático argentino extraordinario) quien me contó hace muchos años que en la Antigüedad (así, tan indefinido y ambiguo como lo que cada uno de nosotros podría interpretar como antigüedad), al no tener la posibilidad de escribir y por lo tanto reproducir, se solían escribir textos en poesía, de manera tal que eso permitiera recordar el supuesto mensaje. Es claramente más fácil recordar una poesía (más allá del tiempo que haya que invertir), que recordar un texto escrito en prosa: ¡de eso no tengo ninguna duda!

Pero al mismo tiempo, esto invita también a pensar que si uno tuviera que recordar algún tipo de secuencia numérica, tratar de encontrar algún tipo de patrón subyacente, sería una vía alternativa muy valiosa y para considerar. Por supuesto, cada persona individualmente elegirá algo que le permita recordar, pero eso era previsible. Cada persona le agregará su particular estilo o historia que para otros, por no decir al resto del mundo no le agregaría nada más que confusión y distracción. Pero como metodología, vale la pena comprender el valor agregado.

Para terminar con esto, lo que sucede es que uno no recuerda un número o conjunto de números, sino lo que recuerda es un ¡evento!, algo particular que tiene un significado personal, intransferible (en general) y único.

 

Final

¿Por qué quise contar esta historia? Como escribí más arriba, no soy muy afecto a recordar nada de memoria. Me produce escozor tener que involucrarme en cuestiones de este tipo. Dicho esto, muchas veces en mi vida, como es muy posible que le debe haber pasado a usted también, queriendo o no, voluntariamente o no, tuve que recordar algo, y tener una idea que sustente la posibilidad de hacerlo o un método que provea alguna herramienta será siempre bienvenida.

Más aún: personas que suelen recordar una tira de números (creo que el récord está en alrededor de mil números consecutivos), lo hace adjudicándoles una suerte de historia, agregándole personajes a cada número (o secuencia de números) que les permite entonces fabricar algo novelado y más fácil de retener. No creo que ninguno de nosotros esté en esa posición, pero, ante cualquier eventualidad, es algo más para tener en cuenta.

Cuando era más joven me preciaba de recordar casi 200 números de teléfonos de memoria, sobre todo de aquellos atletas y/o profesionales cuyo acceso necesitaba por mi profesión. Hoy, estoy muy lejos de poder recordar, no digamos 200, sino que no sé si recuerdo 20. De todas formas, recuerdo libretas de teléfono que teníamos en la radio en la que yo trabajaba, y claramente guardábamos un registro escrito de toda esa información. Hoy, con la tecnología que tenemos disponible, intentar recordarlos parece un esfuerzo totalmente inútil. Sin embargo, ahora estoy convencido de que… ¡no es así! Y si necesitara recordar algo, me gustaría saber que tengo/tendría una herramienta con la que no contaba antes, al menos como una abstracción. Usted… ¿qué piensa?

 

 

 

 

--------------------------------

Para suscribirte con $ 1000/mes al Cohete hace click aquí

Para suscribirte con $ 2500/mes al Cohete hace click aquí

Para suscribirte con $ 5000/mes al Cohete hace click aquí