La Torre de Hanoi

Uno de los problemas más espectaculares y al mismo tiempo famosos de la historia es el que se conoce con el nombre de ‘La Torre de Hanoi’. En realidad, quien lo presentó en sociedad fue Francois Lucas en 1883 como subproducto de una idea que apareció en 1550 en una edición del libro De Subtililate que escribió Girolamo Cardano.

La primera vez que vi este problema fue en una clase de Algebra 1 a cargo de Enzo Gentile, uno de los más maravillosos profesores que tuve en mi vida. El y Luis Santaló nos inundaron e infectaron con su pasión por la matemática. Las condiciones didácticas de ambos los consagraron –según mi perspectiva, claro está— como docentes inigualables. Pero me desvié. La Torre de Hanoi es un problema clásico que aparece en cualquier curso introductorio de álgebra. Yo mismo lo debo haber presentado cientos de veces en mis clases ya sea como ayudante o como jefe de trabajos prácticos o como profesor. No hay forma de eludirlo, ni razones para hacerlo; está omnipresente... ¡y con razón!

Ahora, préstele atención a este texto que es una réplica del original*:

“En un monasterio en Hanoi se tienen tres mástiles, etiquetados con las letras A, B y C. El mástil A contiene 64 discos (como los que se ven en la Figura 1), todos de distinto tamaño y de manera tal que el disco de radio más pequeño está arriba de todos y el de mayor radio es el último, el que está pegado a la base. Los monjes tienen la orden de dios de trasladar todos los discos hasta el mástil C usando la menor cantidad de movimientos posibles y de a uno por vez, pero respetando la siguiente regla muy sencilla: un disco de radio más grande no puede estar apoyado en uno de radio más chico. Los monjes pueden usar los tres mástiles como quieran. Lo curioso es que hay una advertencia: en el momento en el que lleguen a apoyar al último disco, es seguro que habrá llegado “el fin del mundo”. ¿Por qué?”

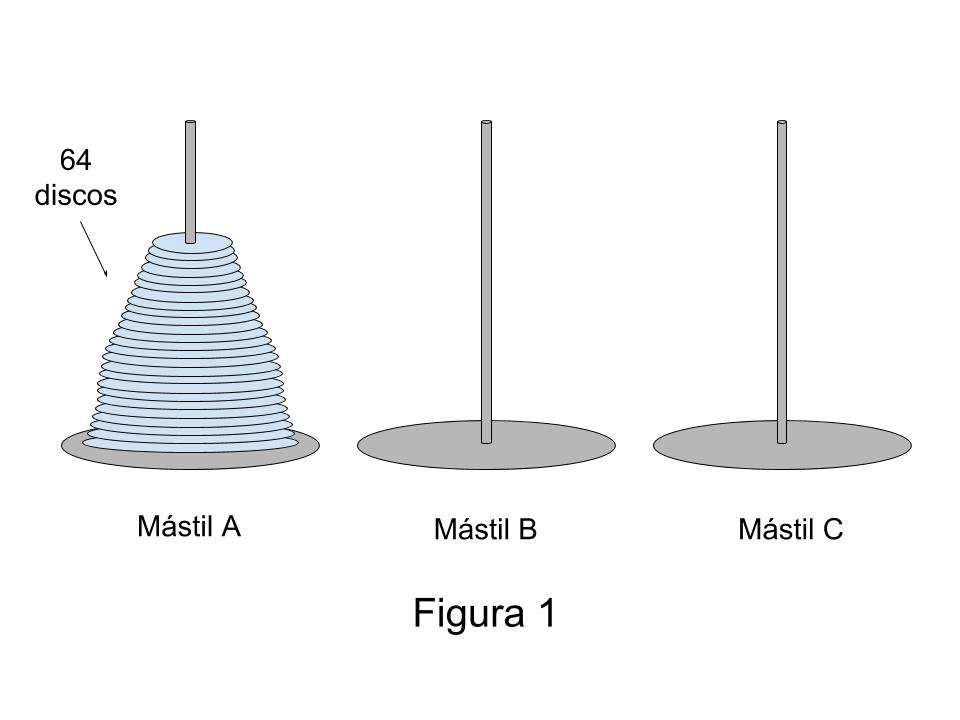
Para entender un poco la mecánica de este problema, le sugiero que empiece con versiones más pequeñas, es decir, en donde el número de discos sea menor que 64 y después usted mismo verá que al incrementar la cantidad de discos adquirirá cierta familiaridad con el problema que le va a permitir entender por qué quien lo escribió imaginó que habría de llegar ‘el fin del mundo’.

Empecemos con dos discos a los que voy a llamar 1 y 2, de manera tal que el número 1 es el de radio más chico y el número 2 es el de radio mayor. Como queda claro del enunciado (y se ve en la Figura 2), el disco 1 está apoyado sobre el disco 2 y ambos están en el mástil A.

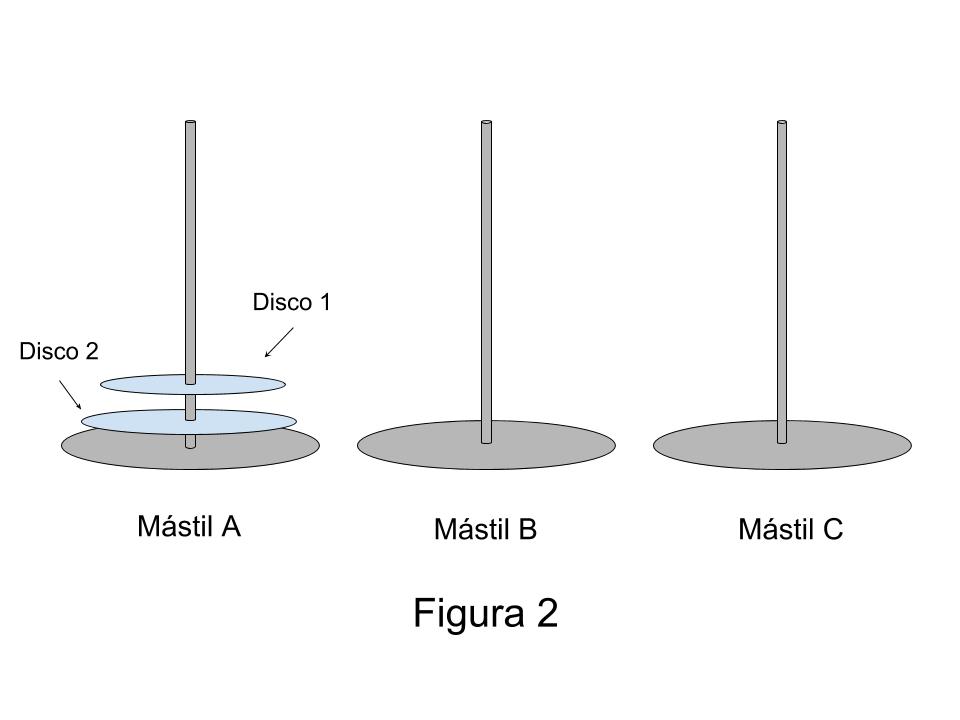
El objetivo es trasladar los dos al mástil C. Como hay que mover los discos de a uno, necesito empezar con el disco 1 pero si lo pusiera en el mástil C, estaría dilapidando un movimiento ya que al disco 2 no lo voy a poder apoyar arriba del uno en ninguna parte del proceso. Por lo tanto, puedo mover el disco 1 hasta el mástil B directamente y avanzar desde allí. La/lo invito a que me siga en este proceso y fíjese qué le parece a usted.

Paso 1: mover el disco 1 al mástil B

Paso 2: mover el disco 2 al mástil C

Paso 3: mover el disco 1 al mástil C y ubicarlo por encima del disco 2..¡y se terminó el problema!

Hemos comprobado entonces que con dos discos fueron suficientes tres pasos (o movidas). Interesante es notar que el mástil B fue utilizado únicamente como intermediario ya que los dos discos originales estaban en el mástil A y al finalizar el proceso los dos terminan en el mástil C.

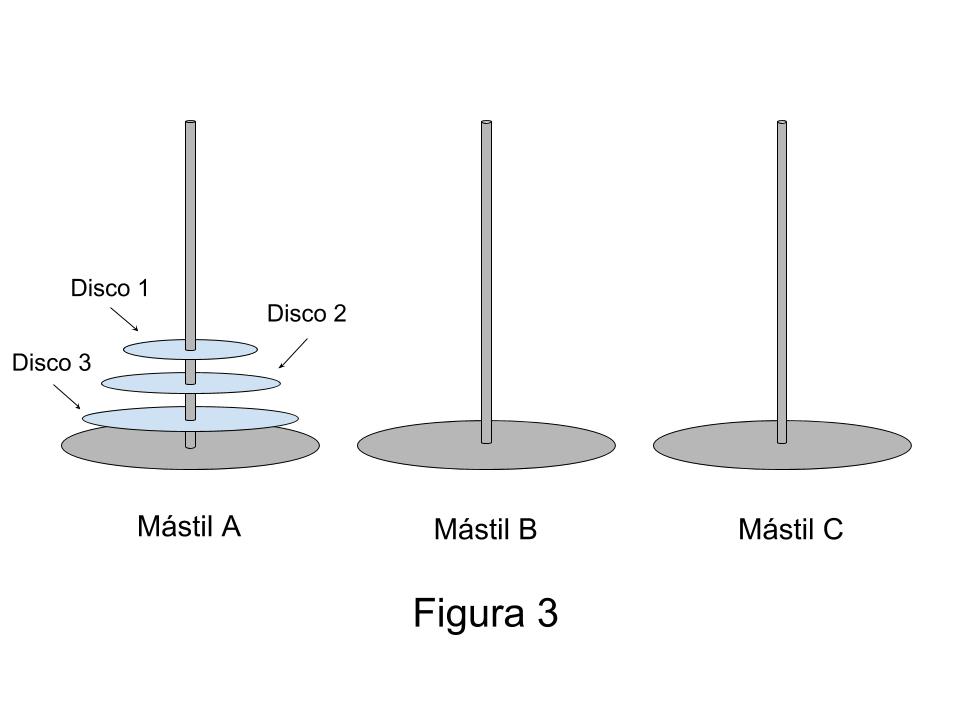
Ahora, aumentemos en uno el número de discos. Los voy a llamar 1, 2 y 3 en orden creciente por el tamaño del radio (el de radio más pequeño es el 1 y el de radio más grande es el 3). Los tres discos están apoyados como se ve en la Figura 3 en el mástil A. Piense usted cómo hacer para hacer el traslado, minimizando el número de movidas y respetando la regla del tamaño. Acá voy yo.

1. mover el disco 1 al mástil C
2. mover el disco 2 al mástil B
3. mover el disco 1 del mástil C al mástil B y ubicarlo encima del disco 2
4. mover el disco 3 del mástil A al mástil C
5. mover el disco 1 del mástil B al mástil A
6. mover el disco 2 del mástil B al mástil C y apoyarlo encima del disco 3
7. mover el disco 1 del mástil A al mástil C y apoyarlo encima del disco 2.

En este caso entonces necesité siete movidas.

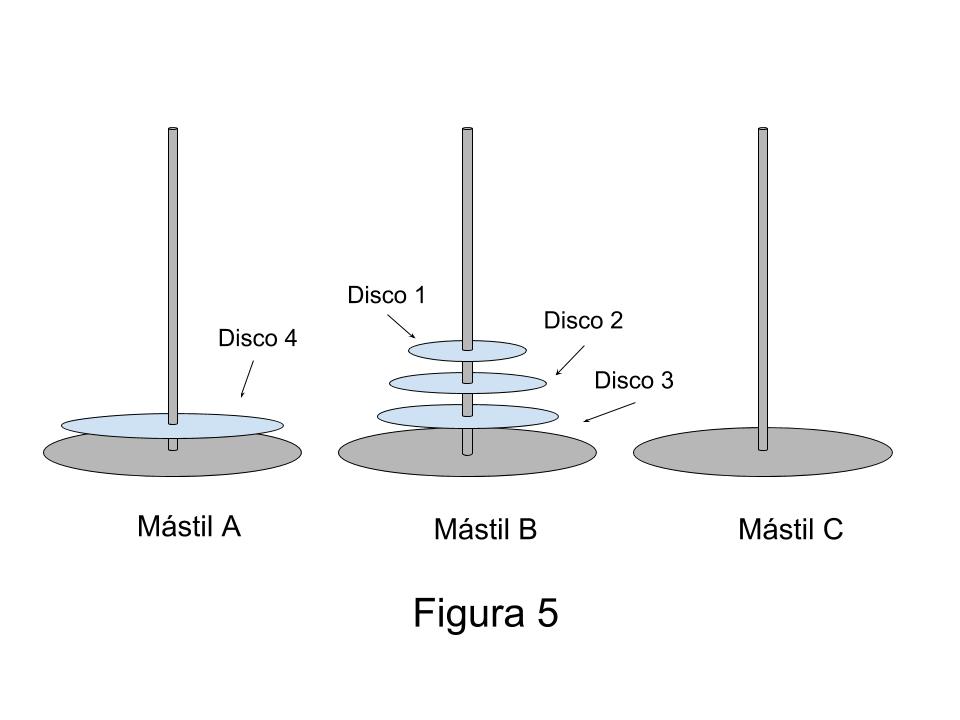
Antes de incrementar en uno el número de discos, quiero hacer una observación que me parece muy importante. Si usted revisa el proceso que acabo de describir, fíjese en la situación que había luego de haber concluido el paso cuatro. Si yo hubiera sacado una ‘foto’ en ese momento, tendríamos lo que aparece en la Figura 4.

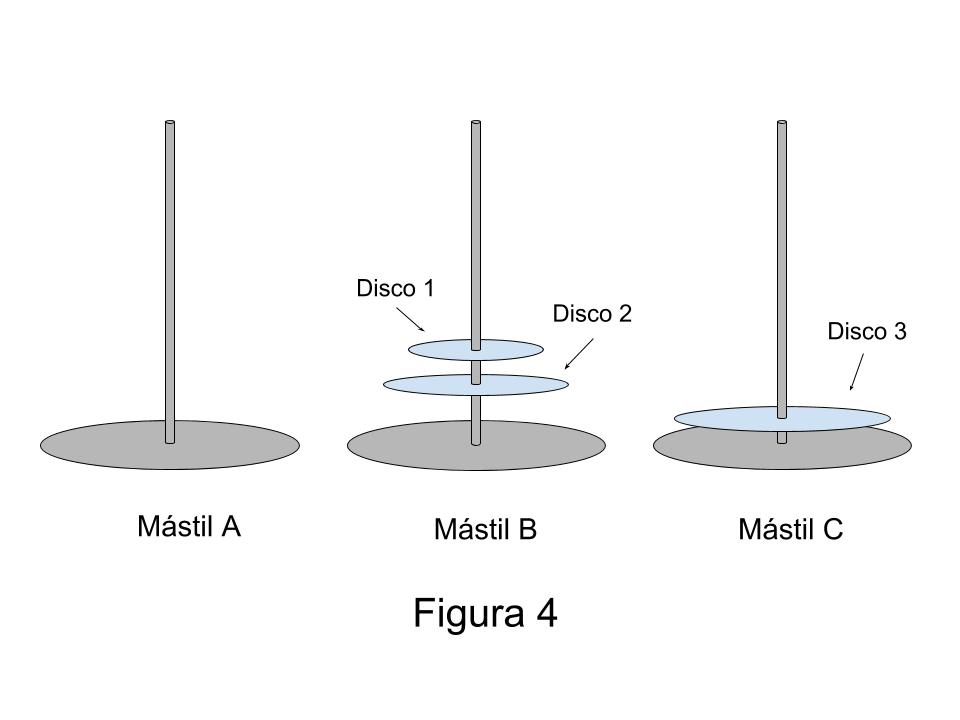
Fíjese que en el mástil C (al que tienen que llegar todos los discos cuando yo termine el proceso), ya está ubicado el disco 3 en su posición final, ya que como es el que tiene mayor radio tiene que quedar abajo de todo. Los otros dos discos (el 1 y el 2), están en el mástil B. Para llegar hasta allí usamos cuatro pasos. Si usted me está siguiendo con el razonamiento, fíjese que esta situación es la que resolvimos al principio de todo, cuando teníamos dos discos para mover, solo que antes estaban en el mástil A y ahora están en el mástil B, pero recuerde también que el mástil que estaba libre en ese momento, lo utilicé solamente como intermediario. Le pido que también recuerde que para pasar dos discos nada más, me hicieron falta tres pasos. Es decir, que si sumara los cuatro pasos que necesité para llegar hasta el momento de esta ‘foto’, con los tres pasos que me faltan, llegaría a los siete que describí más arriba.

¿Por qué me parece importante esto? Porque cuando empiece a agregar más discos, inexorablemente tendrá que haber un momento en que el disco de mayor radio tendrá que estar apoyado en el mástil C por primera vez. No sé cuántos pasos habré necesitado utilizar para llegar a ese momento**, pero seguro que una vez que llegue hasta allí, puedo hacer de cuenta que tengo un disco menos y revisar los pasos que necesité usar para resolver una situación anterior. Todo lo que tengo que hacer es sumar ese número de pasos y tendremos resuelto el nuevo problema.

Si le costó trabajo seguirme en el párrafo anterior, permítame hacer un caso más y verá que cada vez será más claro el camino. Supongamos que ahora tenemos cuatro discos: 1, 2, 3 y 4, en donde 1 es el de radio más pequeño y 4 el de radio más grande. Antes de empezar el proceso, la (o lo) invito a pensar algo junto conmigo. Si tuviéramos nada más que tres discos y no cuatro, yo podría hacer de cuenta que el disco 4 no existe y tengo los tres que están más arriba como los que tengo que trasladar del mástil A al mástil C. Lo interesante es que esta situación ya la sabemos resolver, porque la acabamos de hacer: necesitamos siete pasos para pasar los tres discos del mástil A al mástil C. Como los mástiles B y C son intercambiables, yo podría usar los siete pasos para trasladar los tres discos (1, 2 y 3) del mástil A al mástil B.

Después, necesito un paso más, para llevar el disco 4 del mástil A al mástil C (como se ve en la Figura 6).

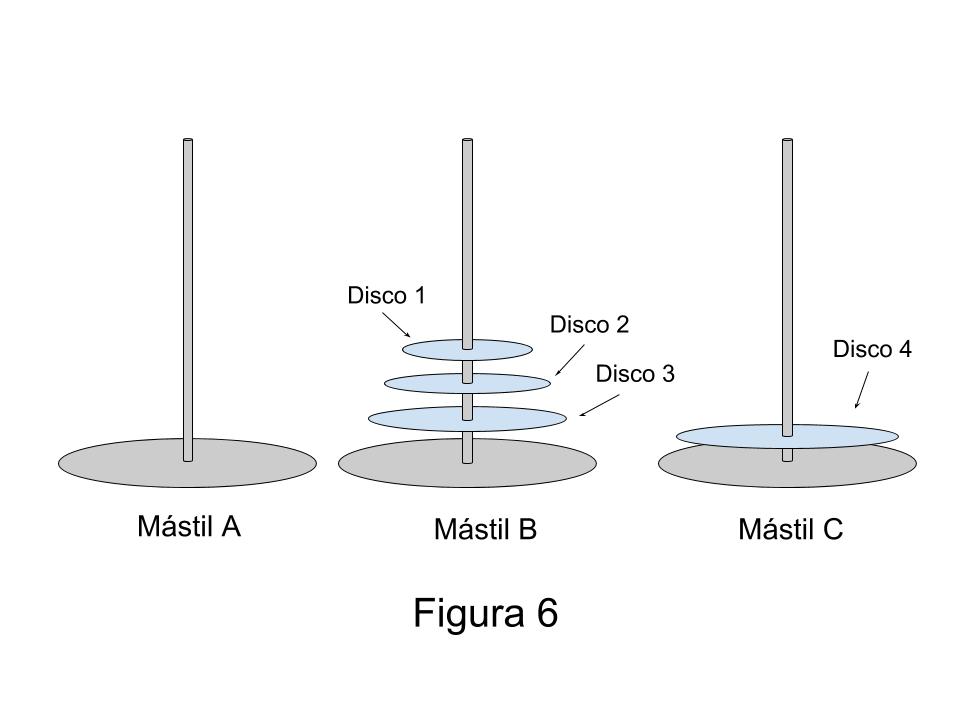
Y ahora, después de ocho pasos, tengo el disco 4 en el mástil C y los tres primeros discos en el mástil B.

A partir de acá, ya sabemos cómo seguir y cuántos pasos voy a necesitar. Como usted habrá detectado, necesito otra vez siete pasos para trasladar los tres discos 1, 2 y 3 del mástil B hasta el mástil C (el disco 4 no se toca y queda quieto en el mástil C desde el momento en el que lo apoyé allí por primera vez).

Moraleja: necesité siete pasos para mover los discos 1, 2 y 3 del mástil A hasta el mástil B. Luego agrego un paso más, para llevar el disco 4 desde el mástil A hasta el C, y para terminar, tengo que agregar siete pasos más, para llevar los tres discos 1, 2 y 3 desde el mástil B hasta el C. Luego de sumar, se deduce que el número de pasos que necesito son: (7 + 1 + 7) = 15 pasos.

Resumen:

1. Para 2 discos, necesitamos 3 pasos.
2. Para 3 discos, necesitamos 7 pasos.
3. Para 4 discos, necesitamos 15 pasos.

No puedo no preguntarle ahora: ¿qué pasará cuando uno tiene 5 discos? ¿No tiene ganas de pensar usted sin mi asistencia?

Sigo… y ahora trato de llegar hasta la solución definitiva.

La estrategia será la siguiente. Supongamos que tenemos discos 1, 2, 3, 4 y 5, todos apoyados en el mástil A. Necesito movilizar los cuatro de arriba hasta el mástil B de manera tal de liberar al disco 5 (que es el más grande). Por lo que vimos más arriba, si yo ignoro el disco 5 y hago de cuenta que solamente tengo que movilizar cuatro discos, necesitamos 15 pasos para llevar los discos 1, 2, 3 y 4 del mástil A hasta el B. Después, un paso más, para trasladar el disco 5 desde el mástil A hasta el mástil C, y por último, necesito otros 15 pasos, desde el mástil B hasta el mástil C. En total, si uno tiene 5 discos, necesita:

15 + 1 + 15 = 31 pasos

Con esta idea, creo que usted está en condiciones de deducir la fórmula general. Fíjese que el número de pasos necesarios está fuertemente relacionado con el número de discos (como no podía ser de otra manera), pero lo interesante es que si uno revisa los números que obtiene son: 3, 7, 15, 31... y estos números, si usted los mira con cuidado... ¡se parecen mucho a las potencias de 2 menos uno! Las potencias de dos son: 2, 4, 8, 16, 32, 64, 128, 256,....etc... y lo que fuimos obteniendo es la misma sucesión de números pero restando uno a cada uno de los números. Y esa es la fórmula general a la que aspirábamos llegar:

“Si uno tiene n discos, le hacen falta (2n – 1) pasos”.

Si usted y yo estuviéramos en el mismo sitio me gustaría decirle lo siguiente:

“Recién hice la cuenta cuando uno tiene ocho discos y necesité 255 pasos. ¿Cuántos pasos te parece que necesitaremos si en lugar de ocho tuviéramos nueve discos?”

Yo aspiraría a que usted (a quien creo muy capaz de encontrar la respuesta) me diga: “Mirá, si ahora tuviéramos nueve discos te invito a que hagamos la siguiente suma: 255 + 1 + 255 = 511. ¿Por qué? Porque necesitaríamos 255 pasos para trasladar (respetando las reglas) los primeros ocho discos del mástil A al mástil B, después un paso más para transportar el disco nueve del mástil A hasta el mástil C y por último, necesitaríamos otra vez 255 movidas para llevar los primeros ocho (que estaban en el mástil B) desde B hasta C. Y listo. ¿Te contesté la pregunta?”

Y mi respuesta sería que sí, que me la contestó. ¿No es extraordinario cómo aparece todo encadenado?

Última reflexión: ¿no siente curiosidad por saber por qué habré escrito en la presentación original del problema que en el momento de completar el proceso con el disco 64 habrá llegado el fin del mundo? ¿Quiere pensar usted por qué?

Es que con 64 discos, harían falta más de 18 ¡trillones de pasos! y si uno utilizara un segundo por movimiento para transportar un disco cualquiera de un mástil a otro, le llevaría unos 58.000 millones de siglos.

Sí, es muy probable que tuvieran razón y que sería el fin del mundo.

 

 

 

---

*La traducción del texto original es mía, por lo que concédame las licencias pertinentes.

**En realidad, sí sé cuántos pasos voy a necesitar, porque será el número de movidas que necesité cuando había un disco menos. Por ejemplo, si se trata de transportar 20 discos, primero tengo que mover los 19 más pequeños, después mover el vigésimo al mástil C y seguir desde allí.

--------------------------------

Para suscribirte con $ 1000/mes al Cohete hace click aquí

Para suscribirte con $ 2500/mes al Cohete hace click aquí

Para suscribirte con $ 5000/mes al Cohete hace click aquí