¿Todos los caminos conducen a Roma?
Antes de que lea la próxima línea, permítame decirle que sí, el nombre Avraham va con ‘v’ corta. Notable, ¿no? Pero es así. La historia que subyace detrás del texto que quiero compartir con usted la generaron dos matemáticos norteamericanos Roy Adler y L. W. Goodwyn, y un israelí, Benjamin Weiss.
Entre los tres plantearon una conjetura (o sea, algo que ellos afirmaban que era así pero que no podían demostrar) que sospechaban que era cierta. Se conoció con el nombre de la Conjetura del Coloreo de las Rutas y como usted verá más adelante si sigue leyendo, es claramente anti-intuitiva.
La presentación en sociedad se produjo en el año 1970 cuando Adler trabajaba para IBM. No voy a poder poner todas las restricciones o hipótesis necesarias para asegurar su validez, pero espero ser capaz de darle una idea de lo que propusieron y juntos recorrer el enunciado para entender cuán difícil es aceptar que el resultado que plantearon sea cierto. Acá voy.
Hagamos de cuenta que estamos en una ciudad. La ciudad no tiene por qué tener ninguna forma ‘convencional’, pero lo que sí tiene que haber es segmentos y vértices (como si fuera una grilla en donde los segmento son calles y los vértices son las intersecciones de esas calles).
Fíjese en la Figura 1. Supongamos que cada vértice es un ‘potencial destino’ (algo así como si hubiera un negocio o una casa o un edificio: un lugar claramente identificable dentro de la ciudad, adonde uno podría querer ir) y por otro lado, los segmentos (que aparecen con flechas que indican la dirección por las cuales uno puede caminar o viajar) son las calles o avenidas, que representan las formas de ir de un destino a otro (de un vértice a otro).
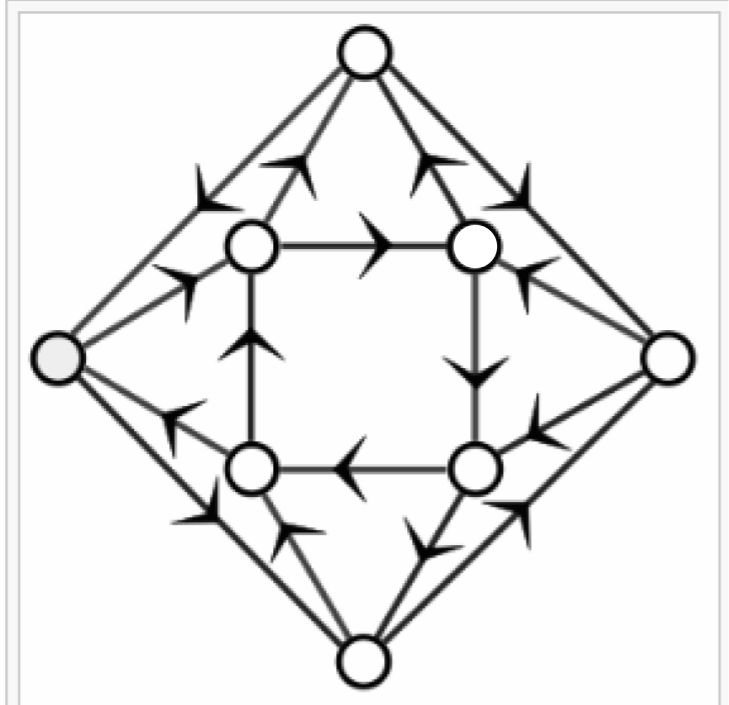
Tome una ciudad cualquiera (como por ejemplo la de la Figura 1). Ahora fijemos (o elijamos) un destino cualquiera (alguno de los vértices), como si distinguiéramos alguno de los círculos. Lo que Weiss y Adler dijeron fue lo siguiente:
“Hay al menos una forma de colorear las calles con algunos colores, de manera tal que ‘siguiendo las mismas instrucciones’ uno llegue siempre al DESTINO que eligió, ¡independientemente del lugar desde donde empieza en la ciudad!”
Me imagino su cara acá, como pensando: “¿Y? ¿Qué dificultad hay?” Parece una estupidez, como si con la mirada me estuviera diciendo: “¿Cómo no voy a poder llegar a un destino prefijado empezando en cualquier lugar?”.
Permítame hacer algunas observaciones y verá que la afirmación no es tan trivial como parece. En principio, bien podría pasar que la ciudad estuviera (por ejemplo) atravesada por un río, y que no haya una calle que cruce de un lado a otro. Evidentemente entonces, si el ‘destino’ está de un lado y usted empieza en el otro, no habrá manera de llegar.
Entendido entonces. Agreguemos una hipótesis que tiene que cumplir la ciudad: habrá que pedirle que esté totalmente conectada. ¿Qué quiero decir con esta terminología? Quiero decir que dados dos puntos cualesquiera de la ciudad (llamémoslos A y B), tiene que haber siempre una forma de ir desde A hasta B pero también en la otra dirección: desde B hasta A.
Pero aun así, no parece muy claro que sea muy difícil. Es aquí donde me interesa que le prestemos atención a una parte de la frase que hice sobresalir en amarillo. La parte que está en verde. Es una parte de la conjetura en donde Weiss y Adler decían que…. “SIGUIENDO LAS MISMAS INSTRUCCIONES”. ¿Qué quiere decir esto?
ESTA es la parte crítica de la conjetura. Me explico.
Para empezar, tenemos que determinar cuál va a ser el DESTINO. O sea, antes de colorear el mapa, necesitamos saber a qué vértice queremos llegar, cuál queremos que sea el destino final. Supongamos por un momento que usted es el que llamé A y es quien vive allí.
Ahora mire la Figura 2, que es la misma que la Figura 1 pero ahora las calles tienen color (rojo o azul) y puse con color amarillo el lugar en donde vive usted.
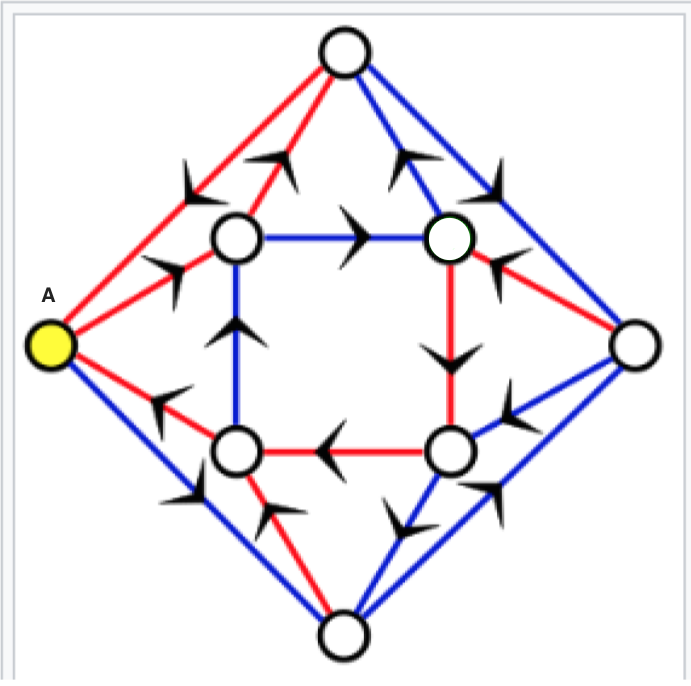
Y acá llegó el momento CRUCIAL. Por favor, elija un círculo cualquiera (que no sea A) y siga estas instrucciones respetando la dirección de las flechas: (azul-rojo-rojo, azul-rojo-rojo y azul-rojo-rojo). Al terminar, usted tuvo que haber recorrido nueve segmentos.
Permítame preguntarle: ¿a qué vértice llegó?
Como usted se da cuenta, cualquiera sea el lugar en donde haya empezado, siguiendo SIEMPRE el mismo camino que yo le indiqué (azul-rojo-rojo, azul-rojo-rojo y azul-rojo-rojo), llegará a A. Inexorablemente. ¿Increíble, no?
Hagamos otro ejemplo. Mire la Figura 3.
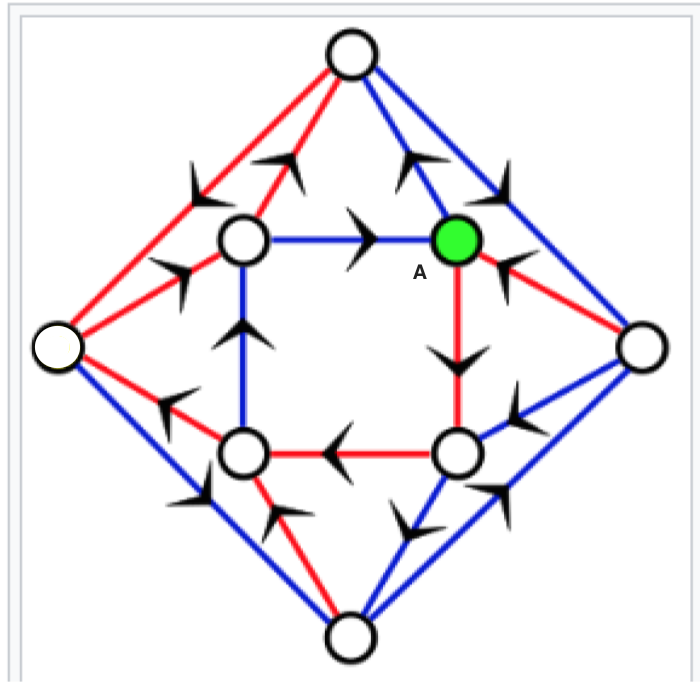
El objetivo ahora es llegar hasta el ‘nuevo’ destino, la ‘nueva’ letra A, que es donde está el círculo de color verde.
Las instrucciones que yo le doy ahora son diferentes: azul-azul-rojo, azul-azul-rojo y azul-azul-rojo.
Una vez más, recorrerá nueve segmentos, pero haya empezado donde haya empezado, terminará SIEMPRE en el círculo verde.
¿Cómo podríamos usar este resultado en la vida real? Supongamos que una amiga suya llega a la ciudad y no sabe dónde queda su casa. Ella puede subirse a un taxi (que tomará en uno de los vértices) y le dirá que siga las instrucciones que usted le dio. Lo extraordinario de esta afirmación es que ella llegará –sin ninguna duda— a su casa, no importa dónde tome el taxi. Ciertamente, a esta altura creo que está claro que la conjetura es fuertemente anti-intuitiva.
La historia para encontrar la solución
Cuando Weiss y Adler plantearon el problema, se lo conoció en el mundo de la matemática como el “Problema del Coloreado de Rutas”*.
Muchos científicos (se estima que más de cien), especialistas en lo que se conoce como Teoría de Grafos, le dedicaron muchos años tratando de demostrar que la conjetura era cierta**, pero por una razón u otra fracasaron en sus intentos. Treinta y siete años después, en el 2007, sucedió un episodio inesperado. Un matemático ruso, Avraham Trahtman, que se había exilado en Israel proveniente de la ex Unión Soviética, logró escribir una demostración. ¿Por qué inesperado? Es que Trahtman, ni bien llegó a Israel, no pudo conseguir trabajo como matemático y durante mucho tiempo trabajó como portero y en áreas de seguridad en diferentes edificios y por lo tanto no pudo avanzar en lo que había sido su especialidad cuando era más joven.
Sin embargo, una vez que logró exhibir la demostración del problema que habían planteado Weiss y Adler, se ocupó de señalar que había tenido suerte y que la solución no era tan complicada sino que era ardua, distinción que le importaba hacer.
Otro episodio que sirvió para mostrar la calidad de persona que es Trahtman es que, si bien podría haber publicado su trabajo en una revista de fama internacional, decidió enviarla al Israel Journal of Mathematics, una revista sin el prestigio de otras que le hubieran dado cabida al resultado que una parte del mundo de la matemática esperaba hacía varios años, pero Trahtman quiso honrar a la gente que le había dado trabajo, muy en particular a Stuart Margolis, un colega que le consiguió un puesto en la Universidad Bar Illan, muy cerca de Israel.
El paper de Trahtman fue aceptado en el año 2007 y publicado en el 2009. Avraham Naumovich Trahtman nació el 10 de febrero de 1944 y vive actualmente en Jerusalem. La publicación de ese solo trabajo lo catapultó a la fama y lo ubicó en un lugar muy distinguido entre los matemáticos que se dedican a la investigación en la Teoría de Grafos.
* Es una traducción libre mía, ya que el original en inglés fue: “The Road Coloring Problem”.
**Una vez más me apuro en decir que hace falta que se cumplan ciertas restricciones. Algunas de ellas: el grafo G tiene que ser finito, estar fuertemente conectado y dirigido y donde todos los vértices tienen que tener el mismo grado de salida (k). Además es necesario que sea ‘aperiódico’.
--------------------------------Para suscribirte con $ 8.000/mes al Cohete hace click aquí
Para suscribirte con $ 10.000/mes al Cohete hace click aquí
Para suscribirte con $ 15.000/mes al Cohete hace click aquí

