Suponga que tiene un tablero de ajedrez (de 8 x 8), donde las casillas no están diferenciadas por color. O sea, son todas iguales… digamos, todas blancas. (Como se ve en la figura 1.)

Vamos a infectar algunas de esas casillas, como si contuvieran alguna bacteria (o algo equivalente) que las transforme en peligrosas. Cada casillero en donde vive alguna de estas bacterias, lo voy a pintar de negro. (Como se ve en la figura 2.)
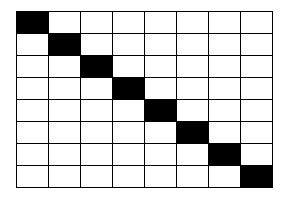
Es decir, algunas casillas estarán infectadas y otras no. Sin embargo, se cumple la siguiente ley: si una casilla tiene hacia alguno de los costados (derecho, izquierdo, arriba, abajo) dos que están infectados, ¡se infecta ella también!
Por ejemplo, si uno empieza con una distribución de casillas infectadas como la que aparece en el caso de la figura 2, al avanzar la infección se tienen (en el primer paso), algunas casillas infectadas más (que corresponden a la diagonal de arriba y de abajo de la que está infectada inicialmente)
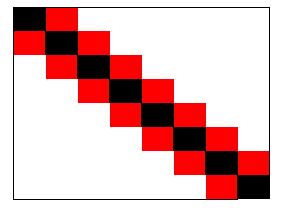
Como usted puede comprobar, si uno siguiera avanzando, infectando el tablero en sucesivos pasos, llegaría un momento en que todo el tablero quedaría infectado.
La pregunta que quiero hacerle es la siguiente:
“¿Es posible empezar con alguna configuración que contenga menos de ocho casilleros infectados, pero que sin embargo, termine infectando todo el tablero?”
Le sugiero que se siente con paciencia y ganas de pensar. Empiece con algunos casos particulares y fíjese si puede infectar todo el tablero. O en todo caso, comience con tableros más chicos (de 3 x 3 o de 4 x 4).
Solución (primera aproximación)
Cuando uno mira los tableros, es razonable hacerse esta pregunta: ¿hará falta que haya por lo menos una casilla infectada en cada fila y en cada columna para que al final quede todo el tablero infectado?
Piense en ese problema primero. Le advierto, por las dudas, que la respuesta es negativa. Es decir, a pesar de que uno —intuitivamente— sospecha que sí, que hace falta que por lo menos alguna casilla de cada columna y de cada fila tienen que estar infectadas, esto no es necesariamente cierto.
Por ejemplo, observe en esta distribución de casillas infectadas:

Avance usted empezando desde allí, y va a descubrir que queda todo el tablero infectado (si no, sígame con las Figuras 4.1 hasta la 4.13 que aparecen al final del artículo).
Es decir, este ejemplo muestra que la primera conjetura no es cierta… Es posible empezar con una configuración que tenga ocho casillas infectadas pero que haya columnas y filas NO infectadas y sin embargo, al avanzar con el proceso de contaminación, se termina infectando todo el tablero [1].
Avanzo.
La pregunta que dio origen a este artículo es: ¿se podrá empezar con menos de ocho casillas infectadas y que sin embargo alcancen para invadir todo el tablero?
No quiero escribir aún la respuesta. Quiero deducirla junto con usted. Para hacerlo, quiero recurrir a un argumento que usamos mucho los matemáticos y por eso me importa exhibirlo acá. Pero me importa (mucho) más que usted me siga. Si no me entendiera en algún punto, pare y vuelva hacia atrás tantas veces como haga falta. Créame: no hay nada imposible de entender. Si lo entiendo yo, lo tiene que poder entender usted también. Además, el recurso (o el razonamiento) que va a descubrir si sigue leyendo, habrá valido la pena.
Justamente, el único placer de pensar estos problemas, reside en descubrir tipos de argumentos que no sólo sirvan para este ejemplo particular, sino que puedan servir para otros casos. De eso se trata.
Para empezar, me quiero poner de acuerdo con usted en algunos nombres. Por ejemplo, fíjese en la figura 5. Voy a usar una grilla de 4 x 4, pero la idea es la misma. El área infectada hasta aquí es de tres casillas, y el perímetro (o sea, si uno suma todos los lados del área infectada) resulta ser 12. No me crea porque lo digo yo: haga la cuenta. Fíjese que si usted suma los lados de cada uno de los tres cuadraditos infectados, llega a 12. (Es que cada uno de los tres cuadraditos tiene cuatro lados, y como no tienen aristas comunes, el número total resulta ser 12.)
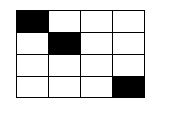
Ahora avanzo un paso más. De la Figura 5 pasemos a la Figura 6. Ahora hay cinco cuadraditos infectados, los rojos y negros.
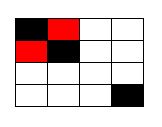
Claramente, el área aumentó: hay más casilleros infectados. Pero… ¿aumentó el perímetro? Haga la cuenta usted sóla/sólo primero.
Tal como usted advirtió (si es que se tomó el trabajo de hacerlo), el perímetro no varió. Sigue siendo doce.
Ahora le propongo que pensemos juntos: una casilla para infectarse, tiene que tener 2, 3 ó 4 casillas a sus costados que ya estén infectadas. Si tiene 2 casilleros infectados a sus costados, esos 2 lados quedarán absorbidos en el área infectada, pero el perímetro no aumenta. Fíjese ahora en las Figuras 7 y 8.

Aquí se ve que hay una casilla que está a punto de infectarse. Eso sucede porque tiene ‘arriba’ y ‘abajo’ dos casillas infectadas. Hasta acá, el perímetro del área infectada es 8 (por ser la suma de los lados de los dos cuadraditos). Sin embargo, en el momento en el que la casilla que está entre las dos se infecte, el lado inferior de la casilla que está más arriba y el superior de la casilla que está más abajo, van a desaparecer. Pero, como usted habrá advertido, esos dos lados van a ser reemplazados por los dos costados (derecho e izquierdo) de la nueva casilla infectada. Es decir, el perímetro, que antes de la infección es de ocho, seguirá siendo ocho cuando el proceso haya terminado, como se ve en la figura 8. (La/lo invito a que cuente usted también por su cuenta para convencerse de que lo escribí es correcto.)
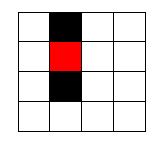
La moraleja es que el área aumento, ¡pero el perímetro no! Sigue siendo ocho.
Si, en cambio, hubiera una casilla con 3 ó 4 de sus costados infectados, el perímetro cambiaría, sí, pero en lugar de aumentar, lo que sucede es que … ¡se va a reducir!
Vea este ejemplo de las figuras 9 y 10
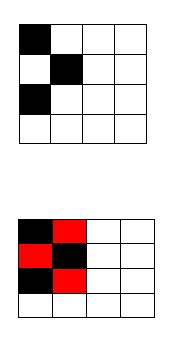
En este caso, en la figura 9 el perímetro es 12, pero al infectar el tablero en la primera casilla, el perímetro se reduce a 10. Es que la casilla de la segunda fila, segunda columna, tiene 3 lados que forman parte del perímetro antes de la infección (figura 9), pero una vez infectada, esos tres lados quedan absorbidos y sólo se agrega 1 a la nueva área. En el camino, se pierden 2 unidades y en consecuencia, el perímetro que medía 12, ahora se redujo a 10.
Después de haber pensado estos ejemplos, le propongo que deduzca conmigo lo siguiente: en cada paso del proceso infeccioso, el perímetro no puede aumentar. Puede que permanezca inalterado o puede que se reduzca, pero lo que es seguro es que… ¡no aumentará!
Ahora falta muy poco. Si aspiramos a que el tablero termine completamente infectado, es porque el perímetro del área contaminada tendrá que ser 32 unidades. Como vimos recién, el perímetro no puede aumentar. Si uno empezara con menos de 8 casillas infectadas, digamos 7, el perímetro infectado inicialmente no puede ser más que 28. Si no puede aumentar, nunca llegará a 32, y por lo tanto, queda contestada la pregunta: no es posible comenzar con menos de 8 casillas infectadas y pretender terminar infectando todo el tablero.
Y una observación más: si uno empezara con 8 casillas infectadas, tiene que tener cuidado de que esas casillas no tengan lados comunes. Si los tuvieran, el perímetro del área infectada sería menor que 32 y ya no habría forma de recuperar esas unidades que uno pierde. De esa forma, y utilizando un argumento totalmente inesperado, hemos contestado la pregunta que motivó este artículo.
Final, muy importante
Como escribí más arriba, este tipo de argumentos es muy común en matemática. Como usted se imagina, si bien todas las posibles configuraciones iniciales son finitas, son ¡muchísimas! Si uno tuviera que probar con todas para convencerse de que no es posible infectar todo un tablero empezando con menos de 8 casillas ‘enfermas’, llevaría mucho tiempo. Es por eso que valió la pena buscar algún otro tipo de argumento que no requiera de utilizar la fuerza bruta.
La ‘batalla’ la ganamos en el momento que descubrimos que el perímetro del área infectada no puede aumentar en el proceso infeccioso. “Esa” fue la clave. El resto es mucho más sencillo. Como uno sabe que el perímetro de todo el tablero es 32, no puede empezar con un área infectada que tenga perímetro menor que 32. Este argumento es el que fuerza a empezar con por lo menos ocho casillas infectadas.
Y ahí reside la belleza de la matemática. Uno puede apelar a un argumento que en principio no parece tener nada que ver (en este caso, el perímetro del área infectada), pero que termina siendo un factor determinante.
Seguro que hay otras demostraciones, pero concédame que la que acabo de presentar acá, es verdaderamente muy bonita.
Apéndice
Tal como escribí más arriba, acá abajo adjunto las 13 figuras que marcan el ‘avance’ de la infección, comenzando con una configuración de ocho casillas infectadas pero en donde hay filas y columnas que tienen todas las casillas ‘sanas’ (no infectadas).


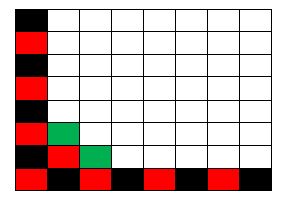
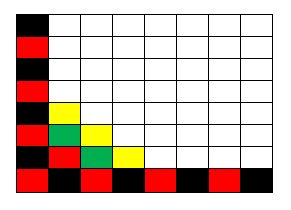
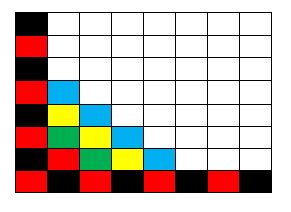
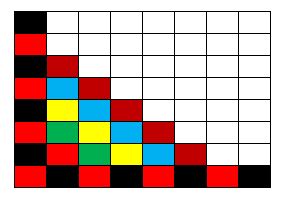
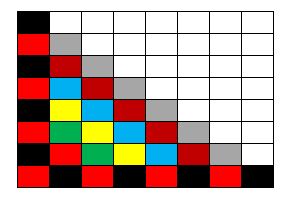
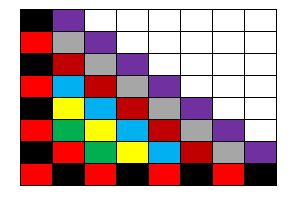
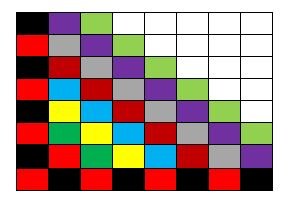



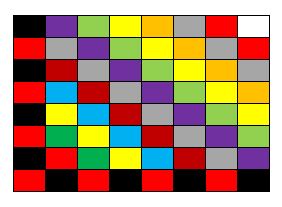
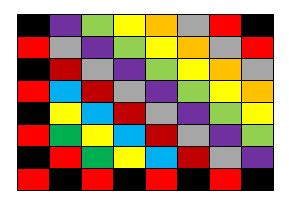
Nota final
El crédito por la existencia de este artículo lo comparten Kvant —una revista soviética (en ese momento)—, una revista húngara (cuyo nombre no conozco), y Peter Winkler, quien lo propuso en un libro que se publicó en el año 2005, Tribute to a Mathemagician.
[1] Hay muchísimas maneras de empezar con ocho casillas infectadas, de manera tal que al terminar el proceso termine infectando a todo el tablero. Siéntese usted y descubra algunas más de las que aparecen en las figuras 2 y 4.
--------------------------------
Para suscribirte con $ 8.000/mes al Cohete hace click aquí
Para suscribirte con $ 10.000/mes al Cohete hace click aquí
Para suscribirte con $ 15.000/mes al Cohete hace click aquí

