El misterio Sudoku

Un pasatiempo que impacta en la cantidad y calidad de la matemática necesaria para abordarlo

Por Adrián Paenza Nov 3, 2019

Para los que lo conocen, y lo probaron, el sugestivo nombre es sinónimo de adicción. Los que todavía se mantienen al margen de la fiebre tienen en esta nota la posibilidad de conocer el “pasatiempo” que inmediatamente los hará prisioneros. Resulta ser una aproximación matemática a la nueva pasión de Occidente. En Oriente ya lleva muchos años entreteniendo humanos.

Pero quiero empezar por el principio: “¿Sudoku, dijo? ¿Qué es 'Sudoku'?” Posiblemente hoy haya mucha gente que pueda contestar qué es el Sudoku, pero hasta hace pocos años nadie tenía idea de lo que habría de transformarse en el “furor” en términos de pasatiempo y juegos de lógica. De hecho muchísimos diarios y revistas —no sólo en la Argentina, sino también en todo el mundo—, tienen sus páginas llenas de este juego originado en Japón, que tiene “atrapada” a buena parte de la población que busca en crucigramas, rompecabezas y pasatiempos de diversa índole; una manera de darle “chicle” al cerebro para mascar.

Para aquellos que nunca escucharon hablar del Sudoku, las reglas son simples y fácilmente comprensibles.

Como es esperable, internet está repleto de variaciones del juego. Su aparición rompió con los moldes de los viejos crucigramas o juegos de palabras tradicionales, pero lo interesante es que si bien aparecen números involucrados (los dígitos del uno al nueve, repartidos múltiples veces en las casillas), pocos deben creer que están usando y haciendo matemática cuando resuelven uno de los problemas. Permítame agregar algo más: cuando usted se propone hacer un crucigrama, inexorablemente necesita saber algo. ¿A qué me refiero? Es que usted no puede intentar resolver palabras cruzadas si no conoce cada palabra cuya definición encuentra a un costado. Dios del sol para los egipcios, por ejemplo, es una sugerencia (bien conocida, por cierto) para que uno escriba RA. O, ‘animal que es el más amigo del hombre, con cinco letras’, es el perro. Si dijera cuatro letras, sería el gato. En fin: está claro que hace falta saber.

Lo interesante es que para jugar al Sudoku… ¡no hay que saber nada! Bueno, no hace falta traer ningún conocimiento previo. Sólo se trata de pensar.

Pero me desvié, como me suele pasar. Como hay muchísimos maestros y profesores de matemática, en los distintos colegios y escuelas del país, que andan a la búsqueda de nuevos estímulos para sus estudiantes, creo que el Sudoku permite hacerse algunas preguntas, no todas de fácil respuesta, que pueden funcionar como “disparadores” de un trabajo “interactivo” entre docentes y alumnos.

Las que siguen son sólo algunas. Eso sí: antes que usted entre en pánico, créame que uno puede jugar al Sudoku sin tener que contestar ninguna, y encima, vivir feliz toda la vida.

Pero también es cierto que uno puede hacerse las preguntas y ser feliz aún sin encontrar las respuestas… y ni qué hablar si las encuentra.

Made in Japan

El nombre Sudoku —de acuerdo con datos extraídos de Wikipedia, la enciclopedia gratuita—, proviene del japonés “Suuji wa dokushin ni kagiru”, que significa: “Los dígitos tienen que quedar solteros”. O “libres”. Sudoku es una marca registrada de la editorial japonesa Nikoli Co. Ltd.

¿Desde cuándo existe el Sudoku?

Hay distintas versiones, pero la más aceptada es que apareció por primera vez en una revista japonesa en 1984. Sin embargo le debe toda su popularidad a Wayne Gould, un juez que se jubiló en Hong Kong y que luego de ver el juego en Tokio, escribió un programa de computadora que automáticamente generaba Sudokus para poder entretenerse él. Luego se dio cuenta de que quizás había descubierto una mina de oro y empezó a ofrecerlo a distintos diarios europeos. Poco tiempo después, en el 2004, uno de los periódicos más importantes de Inglaterra, el Times, aceptó la propuesta de Gould. Y el competidor del Times, el no menos famoso Daily Telegraph, lo siguió inmediatamente en enero del 2005. A partir de ahí explotó en el resto del mundo, incluso en la Argentina. Hoy el juego hace furor en múltiples diarios, revistas, libros especialmente publicados con variantes sorprendentes, versiones más fáciles, más complicadas, con diferentes grados de dificultad. Es común ver gente en los colectivos, trenes, estaciones de subte, ensimismados y pensativos, como “ausentes”, jugando con algún ejemplar del Sudoku. Y encima, es gratis, ¡lo que no es poco!

La matemática

Como decía antes, uno puede sentarse y jugar al Sudoku y entretenerse con él, y nada más. Y de hecho, esto es lo que hace la mayoría de la gente. Pero, al mismo tiempo, resulta desafiante pensar algunas preguntas que uno puede hacerse alrededor del Sudoku.

a) ¿Cuántos juegos de Sudoku posibles hay?

b) ¿Se terminarán en algún momento?

c) ¿Alcanzará para entretener a esta generación? O en todo caso... ¿cuándo empezarán a repetirse?

d) La solución a la que uno llega (cuando llega a alguna)... ¿es única?

e) ¿Cuántos numeritos tienen que venir “de fábrica” para que la respuesta sea única? O sea, ¿cuántas casillas tienen que estar completas de entrada, para que uno pueda empezar a jugar con confianza de que el problema tenga una única solución?

f) ¿Hay un número mínimo de datos que tienen que darnos? ¿Y un número máximo?

g) ¿Hay algún método para resolverlos?

h) ¿Se pueden hacer Sudoku de otros tamaños? ¿Cuántos habrá de 4 x 4? ¿Y de 16 x 16?

i) ¿Se podrán inventar Sudoku de 7 x 7? ¿O de 13 x 13? ¿Por qué no? O, ¿por qué sí? Y en todo caso, ¿cuadrados de cuántas filas y columnas se pueden considerar?

En fin, hay muchísimas preguntas que uno puede hacer, y estoy seguro de que usted, mientras las iba leyendo, pensó otras que le interesan más. En realidad, eso es lo único que importa.

Con todo, quiero aportar algunas respuestas, a las que se puede acceder en cualquier libro que se especialice en este pasatiempo japonés, o bien en internet (ver aparte algunas de las páginas más destacadas) o incluso en la famosa revista Scientific American, que le dedicó una nota de varias páginas en la edición de junio del 2006.

Algunos datos sobre el Sudoku

Me interesa que hagamos algunas reflexiones juntos. Supongamos que usted recién resolvió un Sudoku y decide cambiar dos números de posición. Esto es: cada vez que aparece un número uno, usted lo cambia por un ocho. Y al revés lo mismo, es decir, cada vez que aparece un ocho usted lo cambia por un uno. Obviamente, aunque parezcan dos juegos distintos, son el mismo. Es decir, como juegos son diferentes, pero en esencia uno sabe que uno proviene de otro intercambiando un par de números; por lo que cualquier dificultad que tuviera el primero, lo tiene el segundo. Y viceversa. Ahora bien: cuando tengamos que contar todos los Sudoku que hay, a estos dos últimos, ¿los contamos dos veces o reconocemos que es el mismo con dos “apariencias” diferentes?

Por otro lado, supongamos que uno tiene resuelto un Sudoku e intercambia (sólo por poner un ejemplo) las filas uno y tres. ¿Cambia el resultado final? ¿Agrega o quita alguna dificultad? ¿Y si uno intercambiara la cuarta y la quinta columnas? ¿Varía en algo el planteo inicial? ¿Se trata acaso, de dos juegos diferentes?

Uno puede decir que sí, que son dos juegos diferentes porque las columnas están cambiadas o los dígitos están intercambiados. Aceptemos esta respuesta entonces. En ese caso, si bien es difícil calcular el número de Sudoku sin usar algunas herramientas matemáticas y de lógica (y por supuesto, computadoras rápidas), el número de Sudoku que se pueden encontrar se estima que es:

6.670.903.752.021.072.936.960

o sea, más de 6.670 trillones de posibles juegos.

En cambio, si uno restringe los casos como los que planteé recién, y no considera distintos a los que surgen –por ejemplo– de intercambiar dos dígitos, o dos columnas o dos filas, entonces el número de juegos posibles se reduce muchísimo:

5.472.730.538

O sea, un poco menos de 5.500 millones. Con todo, lo interesante de este número es que —tal como dice Jean-Paul Delahaye en su artículo publicado en Scientific American- es un número menor que el número de habitantes de la Tierra (estimado en más de 7.600 millones).

Con estos datos, está claro que es difícil que uno pueda considerar que se van a acabar los juegos en esta generación. De hecho, creo que estamos en condiciones de jugar tranquilos sin que podamos llegar a descubrir alguna de las posibles repeticiones.

Otra de las preguntas pendientes habla sobre la unicidad en la respuesta. ¿Qué quiere decir esto? Supongamos que a usted le dan un juego de Sudoku que tiene repartidos ciertos dígitos en algunas casillas. Por supuesto, no hay garantía de que la configuración que le dieron tenga solución. Es decir, usted podría encontrarse con algunos datos contradictorios. Pero suponiendo que están bien, y que no hay contradicciones, ¿cómo sabe que la solución que encontró es la única que hay?

En realidad esa es una muy buena pregunta, porque al haber tantos juegos de Sudoku posibles, hay que recurrir a una computadora para poder testear –en general– si hay más de una solución. Podría haber más. De hecho, ustedes mismos pueden inventar uno de estos juegos que tenga más de una solución.

Sin embargo, la unicidad de la solución debería ser un requerimiento básico. Es decir: se supone que si el juego está bien planteado, tiene una solución única. Eso forma parte del atractivo del Sudoku. Si no, sería como jugar al “bingo” y, cuando uno cree que ganó y grita “¡Bingo!”, hay otra persona que “gana” junto con usted.

Ahora bien: ¿cuántos números tienen que venir ya impresos antes de empezar el juego? ¿Los contó alguna vez? ¿Siempre hay la misma cantidad? Lo interesante es que el número de datos con el que ya viene cada Sudoku, varía con el juego. No hay un número pre-determinado que sea “el” correcto. Pero, como usted misma/o puede intuir, algunos números tienen que aparecer porque, en el caso extremo, si no hubiera ninguno, habría muchísimos resultados posibles. Ni bien usted pone un dígito, eso hace disminuir la cantidad de posibles respuestas y, al ir agregando cada vez más, va restringiendo las soluciones posibles, hasta llegar a un número de datos que garantice una solución única.

Otro problema es el que se llama la “minimalidad”. Es decir, ¿cuál es el número mínimo de datos que hay que poner para que haya una sola solución?

Puesto de otra manera: cuando usted se enfrenta con un Sudoku que todavía no ha sido resuelto (como los que aparecen en los diarios), usted advierte que hay varios números que ya aparecen impresos. Diversos grupos de matemáticos en el mundo estuvieron pensando durante muchos años, ¿cuál es el número mínimo que tienen que aparecer de manera tal que exista una única solución?

Hasta hace poco tiempo la conjetura más aceptada era que hacían falta 17 (diecisiete), pero para que eso fuera cierto, era necesario probar —por ejemplo— que no existe ningún Sudoku con 16 números ya distribuidos en la grilla que tuviera solución única.

Llevó mucho tiempo pero al final, en diciembre del año 2011, Gary McGuire, matemático de la Universidad Nacional de Irlanda, Maynooth, lideró el proyecto que lo demostró. Hoy (noviembre del año 2019) sabemos que hacen falta por lo menos 17 números antes de empezar un Sudoku, si uno aspira a que haya una única solución.

McGuire diseñó un programa para correr en una computadora (al que llamó Checker,como si fuera un chequeador) que intentara verificar lo que aspiraba probar. El equipo irlandés necesitó usar más de 7.100.000 horas de tiempo de procesamiento de una computadora. [1]

Estoy seguro de que habrá mucha gente con una tentación particular: preguntarse… “¿No tendrán nada mejor en qué invertir el tiempo, estos muchachos?”

Y la respuesta es un rotundo no. El propio McGuire, en el momento del anuncio, explicó cómo las técnicas utilizadas sirven (o servirán) para tratar problemas en el análisis de expresión de genes, en el estudio de redes de computadoras y aún para el testeo de diferentes softwares. Por lo tanto, las mismas ideas [2] que utilizaron para el Sudoku servirán para mejorar el tiempo de máquina que se necesita aplicar en múltiples disciplinas. En ciencia todo está interconectado, y lo que parece una pérdida de tiempo termina resolviendo un problema en forma impensada. Uno nunca sabe ni cuál, ni cuándo ni donde, pero sobran los ejemplos.

Sigo con el Sudoku. Hay muchas preguntas abiertas (sin respuesta) aún hoy, y hay varios casos más sencillos que se pueden atacar (4 x 4, por ejemplo). Pero lo que me resulta interesante es resaltar cómo un pasatiempo, un juego en apariencia tan inocente, termina teniendo un impacto en otras áreas y además en la cantidad y calidad de la matemática necesaria para abordarlo.

¿Qué es un Sudoku?

Un Sudoku es como si fuera un crucigrama, en donde aparece un “cuadrado grande” de 9 filas por 9 columnas, o sea, de 81 casilleros, que están divididos a su vez, en nueve subcuadrados de 3 x 3. Fíjese en la Figura 1.

Cada “subcuadrado” hay que llenarlo con los nueve dígitos que van del 1 hasta el 9, es decir: 1, 2, 3, 4, 5, 6, 7, 8 y 9. Eso sí: no puede aparecer ningún dígito repetido ni en la misma fila ni la misma columna del “cuadrado grande”. Esas son las reglas, fáciles y sencillas.

Como dato adicional es que ya vienen “de fábrica” algunos números que están ubicados en algunas posiciones. Todo lo que hay que hacer es completar las casillas que están vacías respetando las reglas que escribí en el párrafo anterior.

Por ejemplo:

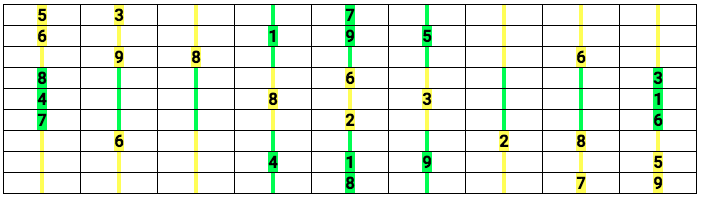
Este es un ejemplo de Sudoku sin resolver. Fíjese que en este caso hay 30 números que ya aparecen ubicados en la grilla. El objetivo, es ubicar los restantes 51 (en total hay 81) de manera tal que no haya repeticiones ni en las filas, columnas ni en los cuadrados de 3x3 que aparecen en amarillo y verde.

La solución la escribo acá abajo:

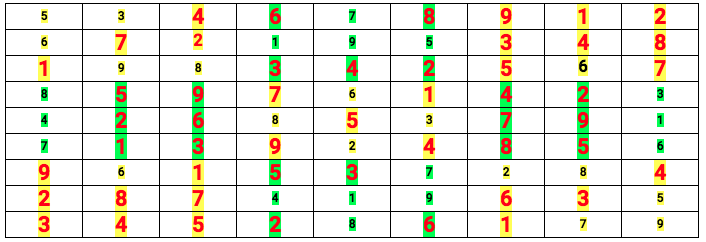
Los números más pequeños y en negro, son los que aparecían originalmente.

Los números más grandes son los que agregué para llegar a la solución.

Pinté de amarillo los nueve números que forman parte de cada subcuadrado de 3x3. Lo mismo hice con los nueve números que pinté de verde: también constituyen un cuadrado de 3x3.

Por si le interesa avanzar más con los Sudokus, la literatura es tan amplia, vasta y profunda. Algunas fuentes que me sirvieron a mí, pero naturalmente, si se decide a entrar en internet y tiene ‘el resto de su vida libre’, no le alcanzará para recorrer todos los sitios en los cuales se puede aprender. Acá van algunos:

[1] Les llevó más de 7 millones de horas usando una computadora con 640 procesadores Intel Xeon hex-core. Empezaron a correr el programa en enero del 2011 y finalizaron en diciembre del mismo año.

[2] El artículo de Gary McGuire, Bastian Rugemann y Gilles Civario se puede encontrar acá: https://arxiv.org/abs/1201.0749

--------------------------------

Para suscribirte con $ 1000/mes al Cohete hace click aquí

Para suscribirte con $ 2500/mes al Cohete hace click aquí

Para suscribirte con $ 5000/mes al Cohete hace click aquí