Hace algunas semanas, en el Aula Magna de la Facultad de Ciencias Exactas y Naturales, hice un cálculo junto con la gente que la habitaba: entre ellos, la decana de la Facultad de Filosofía y Letras Graciela Morgade y el candidato presidencial Alberto Fernandez. En el escenario también estaban ‘casi’ todos los integrantes del Grupo CyTA (Ciencia y Técnica Argentina), becarios... gente ávida por participar.
Mi idea fue la siguiente: si yo pudiera convencer hoy a dos personas para que voten la fórmula FF en octubre, y esas dos personas convencieran (cada una) a otras dos para que hagan lo mismo, en tres días seríamos siete los que nos inclinaríamos por votar esa formula. Si los cuatro nuevos hacen lo mismo al día siguiente y convencieran (cada uno) a dos personas más, la cuenta llegaría a 15 en cuatro días. Siguiendo con este procedimiento, es fácil ver que en bastante menos de un mes llegaríamos a convencer a toda la población de la Tierra.
En algún sentido, sirvió para mostrar cuán rápido crece una progresión geométrica. Si bien uno ‘supone’ qué pasa, cuando la ve en acción en un caso bien específico los resultados parecen asombrosos.
Con la misma idea, quiero contar un problema que está en la mente de los matemáticos desde hace casi 70 años y todavía nadie pudo resolver. El planteo es verdaderamente sencillo [1] y fácilmente comprensible, y enseguida verá por qué. De hecho, la persona que logre resolverlo engrosará su cuenta bancaria en un millón de dólares. Eso es la que está dispuesto a pagar el Clay Mathematics Institute. Pero hay algo más importante aún: la persona que lo resuelva pasará a tener un prestigio singular en el concierto mundial. Créame que hay mucha gente intentándolo, pero hasta ahora sin éxito.
No me abandone ahora porque usted, tanto como cualquiera que pueda y sepa leer, tiene capacidad para entender el enunciado del problema, a tal punto que es difícil de aceptar cómo no se ha podido resolver aún. De hecho, usted verá —si sigue leyendo— que pondrá en duda varias veces que a alguien le puedan pagar semejante suma por resolver lo que parece ser una verdadera pavada. Acá voy.
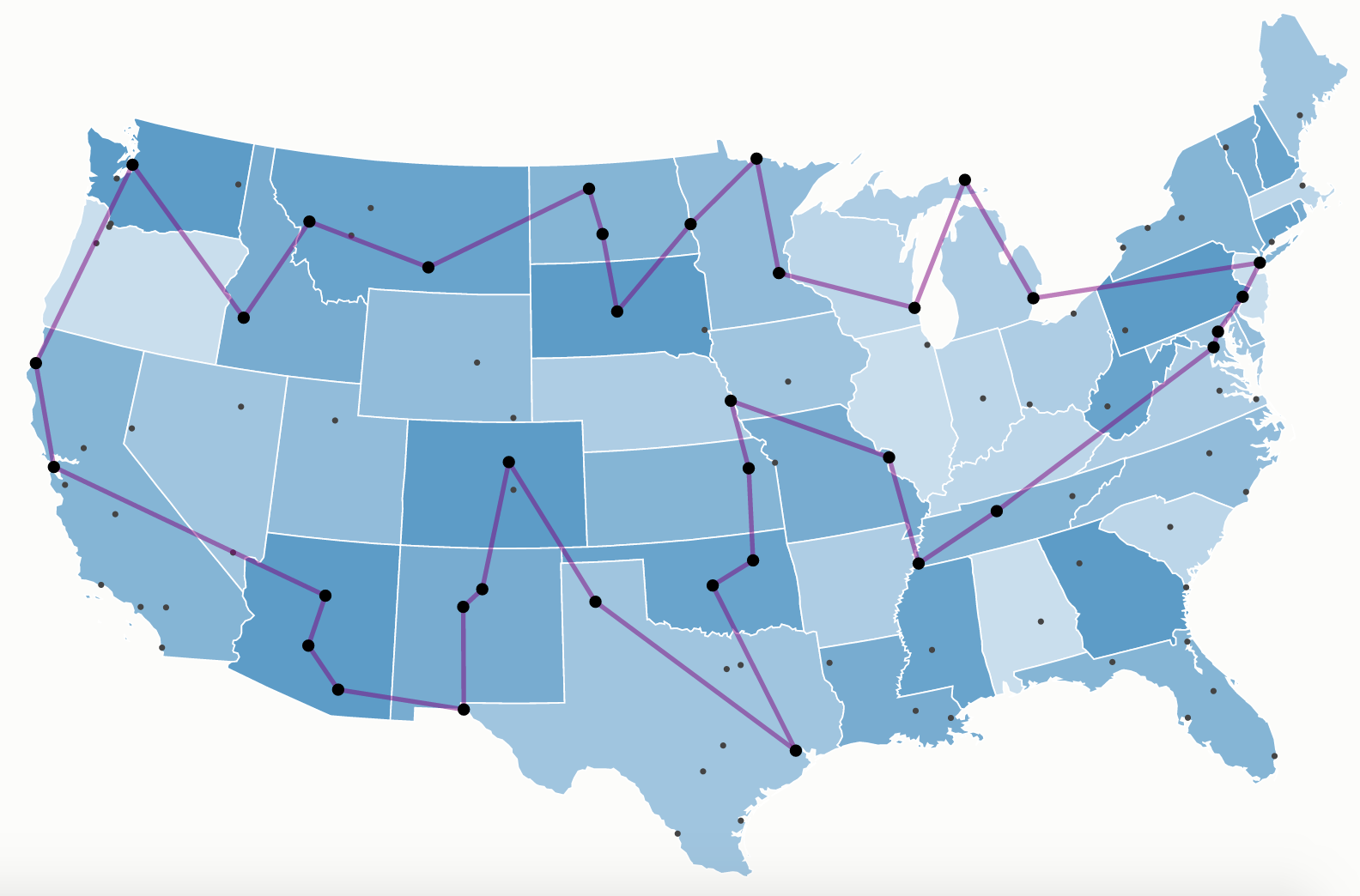
Una persona tiene que recorrer un cierto número de ciudades. Todas están interconectadas (puede ser a través de rutas o carreteras, o por tren o por avión). Es decir, siempre se puede ir de una hacia otra en cualquier dirección.
Además se saben los precios de cada viaje. Es decir: dado cualquier par de ciudades, hay una tabla en donde aparece el dinero que hay que pagar para ir de una hacia la otra. Para hacer las cuentas más sencillas, voy a suponer que el viaje en cualquier dirección sale lo mismo: viajar desde A hacia B cuesta lo mismo que ir desde B hacia A.
Ahora llegó el momento de plantear el problema. Uno puede empezar en cualquier ciudad, no importa cuál . Esa será la ciudad de partida. Desde allí uno empieza un recorrido pasando por todas las ciudades exactamente una única vez (o sea, sin repetir) y luego de recorrerlas todas, vuelve a la ciudad de origen.
Después de haber hecho el viaje, uno suma los precios de cada tramo y está en condiciones de establecer cuánto hubiera costado hacer el viaje eligiendo ese particular orden.
Si uno hiciera lo mismo con todas las posibles elecciones, tendría una tabla con el precio de cada itinerario. Está claro entonces que tiene que haber alguno (o algunos) que sea el más barato. La pregunta entonces es: ¿cuál es? ¿Cómo encontrarlo?
Ya sé: usted debe estar pensando ¿qué tiene de difícil hacer eso? Espéreme un minuto y verá.
Si usted hubiera resuelto el problema tendría que ser capaz de hacer lo siguiente:
“Yo le entrego una lista de n ciudades (no importa el número). Para cada par de ciudades, hay una lista con el precio de lo que sale ir de una a otra. Si usted hubiera resuelto el problema, tendría que ser capaz de decirme cuál debería ser la ciudad de origen y en qué orden tengo que recorrerlas todas, pasando una sola vez por cada una. Al finalizar el itinerario que usted me entregará, yo debería estar seguro de que si sigo sus indicaciones, yo empezaría en una ciudad, pasaría por todas una sola vez y sin repetir, y volvería a la ciudad desde la que empecé. Pero —y esto es muy importante— la ruta que usted me hizo seguir es la más barata de todas. Puede que haya otras que salgan lo mismo, pero ninguna es más barata”.
No hay duda que el problema tiene solución. Esa no es la dificultad. La dificultad reside en encontrar cuál es.
No me diga que no le dan ganas de volver para atrás y leer de nuevo, porque estoy seguro de que a esta altura usted debe dudar de que entendió correctamente el enunciado del problema porque no puede ser que haya una institución que esté dispuesta a compensar con un millón de dólares a la persona que pueda contestar la pregunta.
Una de dos: o usted no entendió bien el planteo o hay algo que anda mal en este mundo.
Sin embargo, está todo bien. Sólo que la dificultad, por ahora, parece escondida.
Los intentos que distintas generaciones de matemáticos han hecho tratando de resolverlo, han permitido múltiples avances, sobre todo en el área de lo que se llama optimización. Pero hasta ahora, septiembre del año 2019, el problema general no tiene solución.
Yo sé que en este momento usted duda de mí, duda de usted… duda de todo. Tiene que haber algo que esté mal. Sin embargo, créame: ¡está todo bien!
Algunos ejemplos sencillos
Para empezar a calentar los motores, le propongo que hagamos juntos algunos ejemplos que involucren pocas ciudades. Verá que en ese caso, todo parece funcionar bien.
Supongamos que se tienen cuatro ciudades, digamos A, B , C y D. Como señalé más arriba, sabemos que ir de A hacia B, cuesta lo mismo que ir de B hacia A. Y lo mismo con todas las otras parejas.
Para ejemplificar, voy a inventar algunos datos, de manera de poder pensar el problema en un caso concreto.
- Costo del viaje AB = 100
- Costo del viaje AC = 150
- Costo del viaje AD = 200
- Costo del viaje BC = 300
- Costo del viaje BD = 50
- Costo del viaje CD = 250
Con esto tenemos cubiertas todos los posibles caminos entre todos los posibles pares de ciudades.
Por otro lado, veamos ahora cuáles son los posibles itinerarios que cubran las cuatro ciudades, pasando una sola vez por cada una y retornando a la ciudad original. Lo invito a que los escriba usted. Por supuesto que también vale seguir leyendo, pero es interesante que usted misma/o se plantee el desafío de escribir todos los itinerarios posibles que satisfacen lo que pedía. Y además, aproveche para contar cuántos son.
Ahora, sigo yo. Acá abajo está la lista:
1) ABCDA
2) ABDCA
3) ACBDA
4) ACDBA
5) ADBCA
6) ADCBA
7) BACDB
8) BADCB
9) BCADB
10) BCDAB
11) BDACB
12) BDCAB
13) CABDC
14) CADBC
15) CBADC
16) CBDAC
17) CDABC
18) CDBAC
19) DABCD
20) DACBD
21) DBACD
22) DBCAD
23) DCABD
24) DCBAD
Todo lo que hay que hacer ahora es escribir los precios de los trayectos (como establece el cuadro 1) y hacer las sumas correspondientes.
| 1-ABCDA | AB = 100 | BC = 300 | CD = 250 | DA = 200 |
| 2-ABDCA | AB = 100 | BD = 50 | DC = 250 | CA = 150 |
| 3-ACBDA | 150 | 300 | 50 | 200 |
| 4-ACDBA | 150 | 250 | 50 | 100 |
| 5-ADBCA | 200 | 50 | 300 | 150 |
| 6-ADCBA | 200 | 250 | 300 | 100 |
| 7-BACDB | 100 | 150 | 250 | 50 |
| 8-BADCB | 100 | 200 | 250 | 300 |
| 9-BCADB | 300 | 150 | 200 | 50 |
| 10-BCDAB | 300 | 250 | 200 | 100 |
| 11-BDACB | 50 | 200 | 150 | 300 |
| 12-BDCAB | 50 | 250 | 150 | 100 |
| 13-CABDC | 150 | 100 | 50 | 250 |
| 14-CADBC | 150 | 200 | 50 | 300 |
| 15-CBADC | 300 | 100 | 200 | 250 |
| 16-CBDAC | 300 | 50 | 200 | 150 |
| 17-CDABC | 250 | 200 | 100 | 300 |
| 18-CDBAC | 250 | 50 | 100 | 150 |
| 19-DABCD | 200 | 100 | 300 | 250 |
| 20-DACBD | 200 | 150 | 300 | 50 |
| 21-DBACD | 50 | 100 | 150 | 250 |
| 22-DBCAD | 50 | 300 | 150 | 200 |
| 23-DCABD | 250 | 150 | 100 | 200 |
| 24-DCBAD | 250 | 300 | 100 | 200 |
Es decir, se tienen en total veinticuatro posibles itinerarios.
Una vez más, todo lo que resta por hacer ahora es sumar los tramos y calcular cuánto cuesta cada viaje. Después uno mira la tabla y decide cuál es el más barato.
En este caso se ve que hay varias soluciones.
Viaje Costo Viaje Costo
1 850 2 550
3 700 4 550
5 700 6 850
7 550 8 850
9 700 10 850
11 700 12 700
13 550 14 700
15 850 16 700
17 850 18 550
19 850 20 700
21 550 22 700
23 700 24 850
El itinerario que habría que elegir es cualquiera de los que cuesta 550. Obviamente, en este caso el problema es de muy fácil solución. ¿Dónde está la dificultad entonces? Falta muy poco para descubrirla, pero en lugar de que lo escriba yo, preferiría que lo hiciéramos juntos.
Hasta acá vimos que con cuatro ciudades hay veinticuatro caminos posibles para analizar.
Supongamos ahora que en lugar de cuatro ciudades, hubiera cinco. ¿Cuántos caminos posibles habrá? (Y acá estará la clave.)
¿En cuántas ciudades se puede empezar el recorrido? Respuesta: en cualquiera de las cinco (A,B,C,D y E).
Una vez elegida la primera, ¿cuántas posibilidades quedan para la segunda ciudad? Respuesta: cualquiera de las cuatro restantes. O sea, nada más que para recorrer las primeras dos ciudades hay ya veinte posibles maneras de empezar:
AB, AC, AD, AE, BA, BC, BD, BE, CA, CB, CD, CE, DA, DB, DC, DE, EA, EB, EC y ED.
¿Y ahora? ¿Cuántas posibilidades hay para la tercera ciudad? Como ya elegimos dos, nos quedan tres para elegir. Luego, como ya teníamos veinte maneras de empezar y cada una de estas puede seguir de tres formas, con tres ciudades, entonces ahora tenemos 60 (sesenta) formas de empezar con tres ciudades. (¿Advierte ya en dónde empieza a estar la dificultad?). Sigo.
Para la cuarta ciudad a elegir, ¿cuántas posibilidades quedan? Respuesta: dos. (Ya que son solamente dos las ciudades que no hemos utilizado en el itinerario que hicimos hasta ahora.) Luego, para cada una de las 60 formas que teníamos de empezar con tres ciudades podemos continuar con dos ciudades. Luego, tenemos 120 (ciento veinte) itinerarios con cuatro ciudades.
Y ahora, para el final, no nos queda nada para elegir porque de las cinco ciudades que había ya hemos seleccionado cuatro: la quinta queda elegida por descarte, es la única que queda.
Moraleja: tenemos 120 itinerarios posibles.
Si usted relee lo que escribimos recién, al número 120 llegamos multiplicando los primeros cinco números naturales:
120 = 5 x 4 x 3 x 2 x 1
Este número se conoce con el nombre 5!, pero no es que se lea con gran admiración, sino que los matemáticos llamamos a este número el factorial de cinco. En el caso que estamos analizando, el número cinco es justamente el número de ciudades [2].
Es fácil imaginar lo que va a pasar si en lugar de tener cinco ciudades, se tienen seis. El número de caminos posibles será:
6! = 6 x 5 x 4 x 3 x 2 x 1 = 720
Sigo un par de pasos más.
Siete ciudades, 7! = 5.040
Ocho ciudades, 8! = 40.320
Nueve ciudades, 9! = 362.880
Diez ciudades, 10! = 3.628.800
Y paro acá. Como usted se da cuenta, el total de rutas posibles que habría que analizar con sólo diez ciudades es de ¡más de tres millones seiscientos mil!
La primera conclusión que uno saca es que el factorial de un número aumenta muy rápidamente a medida que uno va avanzando en el mundo de los números naturales. Tan rápido aumenta, que lo invito a que usted haga las cuentas para convencerse.
Imagine que ahora usted es un viajante de comercio y necesita decidir cómo hacer para recorrer las capitales de las 22 provincias argentinas, de manera tal que el costo sea el menor posible. O sea, de acuerdo con lo que vimos recién, habría que analizar
1.124.000.727.777.610.000.000
rutas posibles (más de mil cien trillones). ¿Por qué? Es que el factorial de 22, es justamente este número que escribí recién:
22! = 1.124.000.727.777.610.000.000
Por lo tanto, usted estará de acuerdo conmigo: para resolver el problema hace falta tener una computadora muy potente. Pero aún así, este ejemplo (el de las 22 capitales) es muy pequeño.
Creo que ahora queda clara la dificultad. No reside en hacer las cuentas ni en el método que hay que emplear. ¡Esa es la parte fácil! Es que hay que sumar y luego comparar.
Pero el problema, insalvable por ahora, es que hay que hacerlo con muchísimos números, un número enorme, que aún en los casos más sencillos, de pocas ciudades, parece inabordable.
Lo que se intenta hoy es tratar de encontrar alguna manera de encontrar la ruta más barata sin tener que hacer todos los cálculos, sumar y luego comparar. Ya con 100 ciudades se sabe que el número de itinerarios posibles es tan grande, que ni siquiera las computadoras más poderosas pueden manejarlo. Hay varios casos particulares que fueron resueltos, pero en esencia, el problema está abierto.
Un último comentario: con los actuales modelos de computación, el problema no parece que tenga solución. Hará falta entonces, que aparezca alguna nueva idea que revolucione todo lo conocido hasta acá.
Nota
Supongamos que uno tuviera 100 ciudades. No parecen tantas para un viajante de comercio, ¿no es así?
En ese caso, el número de itinerarios posibles se calcula estimando el ‘factorial del número 100’. Ese número tiene (y lea bien, porque no me equivoqué) 157 dígitos. Si le interesa ‘verlo’, es este:
93,326,215,443,944,152,681,699,238,856,266,700,490,715,968,264,381,621,468,592,963,895,217,599,993,229,915,608,941,463,976,156,518,286,253,697,920,827,223,758,251,185,210,916,864,000,000,000,000,000,000,000,000
Es decir, este número indica la cantidad de ‘potenciales itinerarios’: ¡son muchos!
Como escribí más arriba, si usted toma cualquier par de ciudades, la ‘tabla’ que yo le entregué tiene asociado un ‘precio’ para viajar entre ambas (no importa en qué dirección).
Lo que la computadora tendría que hacer, es sumar todos los ‘tramos’ y determinar el ‘precio’ del viaje.
Acá es donde quiero agregar algunos datos que me parecen esenciales. (Y le pediría que no pare de leer justo ahora.)
Las computadoras más rápidas que existen pueden calcular el precio de un millón de itinerarios por segundo. De nuevo: ¡un millón de itinerarios por cada segundo! Son increíblemente rápidas.
Sin embargo, si una de ellas se propusiera analizar todos los itinerarios posibles tardaría
2,9 * 10142 siglos
No espero que usted pueda leer este último número, pero para tener una idea, sería como tener un número 3 al que le siguen ¡142 ceros! Y esos serían los siglos necesarios.
Supongamos que las computadoras se hicieran más rápidas, mucho más rápidas, digamos 10.000 veces más rápidas. Por lo tanto, en lugar de analizar un millón de itinerarios por segundo, pudieran analizar 10.000 millones de rutas por segundo.
Aún así, analizarlos todos, le llevaría ahora un número 3 seguido de 138 ceros, y eso indicaría la cantidad de ¡siglos!
Es decir, si la aspiración es que el problema se resuelva mientras nosotros construimos computadoras más rápidas... ¡perdimos! Ese no puede ser el camino.
Uno podría pensar: ¿por qué hacerlo con una sola computadora? ¿Por qué no poner muchas a trabajar al mismo tiempo? Lo que sigue, creo, le va a ayudar en la respuesta.
Los físicos sostienen que en el universo hay algo así como 1082 partículas, o sea, un uno seguido de 82 ceros...
Si cada una de esas partículas se convirtiera súbitamente en una computadora, aún así, necesitaríamos (si todas trabajaran al mismo tiempo)
1.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000.000 SIGLOS
Así no va a funcionar. Quienes se dedican a este tipo de problemas, buscando algoritmos que permitan resolver problemas como el del ‘Viajante de Comercio’, saben (aunque no puedan probar) que ¡este no es el camino!
Tendrá que venir ‘alguien’, que sea capaz de proveer una idea que hasta acá no apareció, y que ‘dé vuelta todo como una media’. Mientras tanto, ¡el millón de dólares seguirá sin dueño!
Algunos datos útiles
- El problema general, conocido como TSP (Travelling Salesman Problem, Problema del Viajante de Comercio) fue estudiado por primera vez alrededor de 1930 por Karl Menger en Viena y en Harvard.
- En 1954 se publicó una solución para 49 ciudades, en 1971 para 64 ciudades, en 1975 para 67, y luego, en los últimos cuarenta años, hubo saltos cuantitativos más importantes, que permitieron pasar de 318 a 532, luego a 666 y 2392 (en 1987), 7397 (1994), 13.509 (en 1998), y voy a agregar dos más: para 15.112 ciudades hubo un aporte en el año 2001 y en el año 2004, se resolvió el caso para ‘casi’ 25.000 ciudades. En realidad, un grupo de científicos suecos publicó el caso en que se tienen 24.978 ciudades. Si usted está interesado en este caso particular, la referencia la puede encontrar acá: http://www.tsp.gatech.edu/history/tspinfo/sw24978_info.html)
- Para aquellos que conocen un poco más del problema y/o son especialistas o matemáticos: he omitido adrede la discusión sobre P versus NP (polinomiales vs ‘no-polinomiales’) simplemente porque en este contexto no agrega nada. En cambio, creo, la presentación de esta forma sirve para exhibir el centro de la dificultad: ¡lo rápido que crece el factorial de un número!
- En la página oficial del Clay Mathematics Institute (http://www.claymath.org/millennium/P_vs_NP/), se propone el problema de la siguiente manera: “Suponga que usted tiene que ubicar en un hotel en el que sólo caben cien personas a un grupo de cuatrocientos estudiantes. Usted sabe que sólo cien tendrán en donde alojarse. Bien, pero ¿cuáles? Encima, el decano del colegio le advierte que hay ciertos pares de estudiantes que no pueden estar juntos, porque no se llevan bien. Este es un ejemplo de lo que los computadores llaman un problema NP, ya que es fácil determinar, si alguien le trajera una distribución posible, si satisface o no las restricciones. (O sea, si ningún par de los prohibidos figura en la lista.) Sin embargo, la tarea de generar esa lista desde el principio parece mucho más complicada e impráctica (sic). De hecho, el número total de maneras de elegir los cien estudiantes entre los cuatrocientos que hay, es un número más grande que el de todos los átomos del universo. Por lo tanto, ninguna civilización futura podrá construir una supercomputadora que sea capaz de resolver el problema por la fuerza bruta, o sea, chequeando a mano toda posible combinación de 100 estudiantes” Y sigue: “Hasta aquí nadie ha logrado probar que el problema sea tan difícil como parece, es decir, que no haya una manera razonable de generar una respuesta con la ayuda de una computadora”. Por último, Stephen Cook y Leonid Levin describieron en el año 1971 y en forma independiente dónde radica la dificultad, entre los problemas llamados P (cuya solución es fácil de encontrar), versus los llamados problemas NP (que son los fáciles de chequear).
[1] El problema se conoce con el nombre TSP, por su sigla en inglés: Travelling Salesman Person, o sea, el Problema del Viajante de Comercio.
[2] Se le pone un nombre a esta operación, que resulta de multiplicar los primeros n números naturales (el factorial de ‘n’) porque es una situación que aparece muchas veces cuando uno tiene que contar conjuntos finitos. O sea, tiene sentido llamar de alguna manera al producto de los primeros números naturales. Por ejemplo,
3! = 3 x 2 x 1 = 6
4! = 4 x 3 x 2 x 1 = 24
5! = 5 x 4 x 3 x 2 x 1 = 120
10! = 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 x 1 = 3.628.800
--------------------------------
Para suscribirte con $ 8.000/mes al Cohete hace click aquí
Para suscribirte con $ 10.000/mes al Cohete hace click aquí
Para suscribirte con $ 15.000/mes al Cohete hace click aquí