El reloj de Fibonacci

El tiempo siempre es el mismo. Pero hay maneras insólitas de medirlo.

 

Hace muy poco se cumplieron 16 años de una charla que fue una de las más concurridas de la historia de nuestra facultad, Exactas (UBA). Fue en el aula magna del Pabellón dos y más que una conferencia fue una ‘fiesta’. Participamos ‘todos’ y cuando escribo ‘todos’ es porque no hubo —virtualmente— ningún tipo de distinciones. Vinieron (y se involucraron) estudiantes de todas las carreras que se cursan allí y también profesores de los diferentes departamentos (Matemática, Física, Ciencias de la Computación, Química, Geología, Biología, Ciencias de la Atmósfera...). Había gente sentada en los pasillos, otros participaron de pie en lugares desde donde (me consta) se podía escuchar, pero no se podían ver los pizarrones... Algo así como un sueño. El tema fue “La Sucesión de Fibonacci y el Número de Oro”.

La duración habitual de una charla de divulgación de estas características es de alrededor de una hora, pero esa vez estuvimos allí más de cuatro y terminamos sólo porque había que apagar la luz y los colectivos ya no habrían de llegar más hasta la Ciudad Universitaria. Fue un momento maravilloso y en alguna oportunidad voy a tratar de escribir un resumen de lo que allí se dijo, tarea ciertamente imposible si pretendo que sea exhaustiva. Pero, como siempre... me desvié.

Antes que se ‘asuste’ pensando en que usted nunca ni siquiera escuchó hablar de la sucesión de Fibonacci, permítame decirle que no hace falta ‘saber nada’. Un poco más adelante, en el apéndice, escribí algunas de las explicaciones más elementales, pero usted puede avanzar con el texto sin ninguna dificultad.

Sin embargo, como las aplicaciones sobre la sucesión de Fibonacci son tan variadas y en tantas áreas ([1]), que cada tanto me sorprendo leyendo algunas de las novedades. Hace unos días me tropecé con la página web ([2]) de un diseñador canadiense, Philippe Chrétien. Llegué hasta allí porque Philippe está (o estaba) tratando de juntar fondos para lanzar una compañía que le permitiera producir en serie un reloj que llamó ‘El Reloj de Fibonacci’. Eso solo ya me invitó a ver el video en el que muestra cómo lo construye ([3]), pero lo que me tenía confundido es que no podía deducir cómo funcionaba. Es decir: todo muy interesante, diseño, estética, colores, hasta incluso el ‘nombre’, pero para que se llame reloj, al menos por ahora, hace falta que ‘marque la hora’, ¿no?

Cuando finalmente comprendí lo que hacía, me pareció que sería interesante compartirlo. Esa es la historia que quiero contar acá.

En principio, la sucesión de Fibonacci consiste en una cantidad ‘infinita’ de números (naturales). Los primeros términos son los siguientes:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, .....

Ahora, vaya hasta la Figura 1. La foto que usted ve es el resultado final, el reloj ya terminado.

Si le presta atención al diseño verá que hay claramente marcados cinco cuadrados. El más grande (en área) es el de color azul que está apoyado sobre la derecha del rectángulo y mide (5 cm x 5 cm). El segundo más grande es el verde, que también está apoyado en la base y mide (3 cm x 3 cm). Luego hay otro un poco más chico, también azul, que mide (2 cm x 2 cm), y dos cuadraditos iguales (rojo y blanco), cuyas dimensiones son (1 cm x 1 cm), como se ve en la Figura 2.

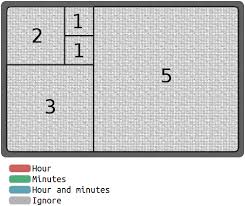
Acá aparece el primer dato interesante: tanto los lados de los cuadrados como los de la caja se corresponden con los primeros números de la sucesión de Fibonacci: 1, 1, 2, 3, 5 y 8. Como usted ve, los cinco primeros números se corresponden a las medidas de los lados de los cuadrados. Por otro lado, tanto la base del rectángulo (ocho) como su altura (cinco) son también números de la misma sucesión. No incluyo la profundidad de la caja, primero porque no la sé y segundo porque no participa en ‘comunicar’ la hora.

Ahora, le pido que me tenga un poco de paciencia y verá que todo comenzará a tener sentido.

La pregunta que todavía sigue/sigo sin contestar es: ¿cómo hace esta caja rectangular con los cuadrados incluidos para marcar la hora?

Vea qué interesante lo que se le ocurrió a Philippe. Diseñó el reloj de tal manera que detrás de cada cuadrado hay una ‘lámparita’ (que uno no puede ver). Cada una de las cinco lámparas puede estar apagada o encenderse de tres colores diferentes: azul, verde y rojo. Si está apagada, el cuadrado queda de color ‘blanco’.

Ahora bien: ¿cómo hacer para combinar las luces encendidas y/o apagadas, de manera tal que los colores que uno pueda ver desde afuera, sirvan para conocer la ‘hora’? Ese es el desafío.

En principio, lo primero que uno tendría que poder es ‘fabricarse’ todos los números que indican las ‘horas’. Para eso, voy a elegir algunos de esos cinco números (1,1,2,3,5) que son las medidas de los ‘lados’ de los cuadrados del reloj y los voy a sumar de diferentes maneras. Mi objetivo, como indiqué acá mismo, es que al combinarlos y encenderlos con el mismo color, pueda generar los doce números necesarios para marcar las horas: 1,2,3,4,5,6,7,8,9,10,11 y 12. Fíjese en esta lista:

1 = 1

2 = 2

3 = 3

4 = 3+1

5 = 5

6 = 5+1

7 = 5+2

8 = 5+3

9 = 5+3+1

10 = 5+3+2

11 = 5+3+2+1

12 = 5+3+2+1+1.

Por supuesto, no hay una única manera de obtenerlos. Por ejemplo, el seis puede obtenerse como (5+1), pero también como (3+2+1). Sin embargo, lo que importa es que los doce números se pueden obtener al menos de una forma.

Si el reloj tuviera que solamente marcar las horas, el problema estaría resuelto (y ni siquiera harían falta tantos colores). Bastaría con encender los cuadrados que uno quiere que intervengan en la suma y dejar los otros apagados. Pero el problema es un poco más complicado, porque además de las horas, uno tiene que ‘indicar’ cuáles son los minutos.

Acá surge un inconveniente: si bien las horas las pudimos obtener combinando los cuadrados que van a estar encendidos, lo pudimos hacer porque hay nada más que 12 números. En cambio, para los minutos, necesitaríamos combinar esos mismos cuadrados para obtener todos los números entre 1 y 59. Ese problema también tiene solución, pero uno necesitaría hacer un curso para recordar qué número corresponde a cada combinación de luces y colores encendidos. Es por eso que a Philippe se le ocurrió una idea muy peculiar. Acompáñeme por acá y verá que es una idea muy interesante.

Cuando usted consulta la hora, digamos en el reloj de su teléfono celular o en algún otro tipo de reloj digital, ¿le presta atención a los segundos? Es decir, cuando su reloj marca —por ejemplo— la 1 y 10 de la tarde, hasta que la hora no llegue a 1 y 11, usted no se ‘entera’ de los ‘segundos’. En algún sentido, uno se concede la licencia de resignar la exactitud de los segundos y va dando ‘saltos’ de un minuto.

Lo mismo hizo Philippe, pero se permitió una licencia un poco mayor: los ‘saltos’ son de cinco minutos en lugar de uno.

Me explico: el reloj no va a marcar con precision la hora ‘exacta’, sino que se mantiene ‘quieto’ durante cinco minutos. Por ejemplo, en un momento determinado marca las 5 y 10... y allí se queda hasta llegar a las 5 y cuarto. En ese momento pasa a marcar las 5 y 15. Allí se queda ‘quieto’ durante cinco minutos otra vez, y recién entonces, marca las 5 y 20. Y así siguiendo.

Está claro entonces que el reloj de Fibonacci no es un reloj convencional. Es ciertamente bien distinto de lo que uno acostumbra a ver. Así como uno acepta errores de un minuto en un reloj ‘pulsera digital’ que no tiene segundero, lo mismo hay que hacer ahora, pero con ‘saltos’ de cinco minutos en lugar de uno. Si usted hace la cuenta, verá que —en general— los relojes sin segundero cambian 60 veces por hora. En este caso, el reloj cambia solamente doce veces por hora ([4]).

Aceptada esa ‘licencia’, sigo con el relato y con la idea de Philippe.

Como los cuadrados pueden estar iluminados de diferentes colores, estas son las reglas:

* para saber las horas, hay que sumar los cuadrados ([5]) que aparezcan en color rojo y azul;

* para saber los minutos hay que hacer dos pasos: primero, hay que sumar los cuadrados que aparezcan en verde y azul. Como segundo paso, a ese número, ¡hay que multiplicarlo por 5! Esto dará el número total de minutos que uno busca.

Ya sé.. ya sé... ¿Multiplicar por 5? Sí, multiplicar por 5. Verá que es muy sencillo. Es mucho más complicado de ‘describir’ que de ‘entender’, pero si usted ‘relee’ lo que acabo de escribir, verá que los cuadrados azules intervienen tanto en las horas como en los minutos. En cambio, los rojos aportan NADA MAS que para las horas y los VERDES, aportan NADA MAS que para los minutos.

Ahora sí, acá están los ejemplos (que imagino que usted me está reclamando). ¿Puedo pedirle un favor?... ¡No se pierda ahora! ¡Falta muy poco y sería una pena que si llegó hasta acá, ahora se pierda lo mejor! Acá voy.

Tómese un par de minutos y verá que todo es muy sencillo.

Fíjese en estos dibujos y tenga a mano las ‘reglas’ que acabo de escribir.

 

Ejemplo 1

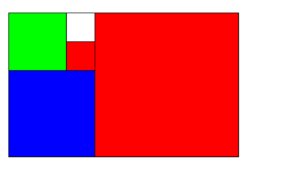
Si este fuera el frente del reloj de Fibonacci, ¿qué hora indicaría?

Sigamos las instrucciones. Para determinar las horas, hay que sumar los cuadrados rojos y azul. Encendidos de rojo están los cuadrados de longitudes 5 y 1. Encendido de color azul, está únicamente el de 3. Total: 5 + 1 + 3 = 9.

Para determinar los minutos, hay que, primero, sumar los cuadrados de colores verde y azul. De color verde, está solamente encendido el de 2 y el de azul, el de 3. En total, sumando 3+2 = 5. Pero.. ¡este no es todavía el número de minutos, sino que todavía falta multiplicar por 5! ¿Resultado? El número de minutos entonces es…¡25!

En definitiva la hora que marca el reloj de Fibonacci son las ¡9 y 25!

 

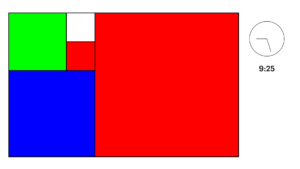
Ejemplo 2

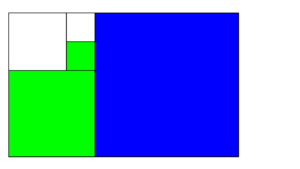
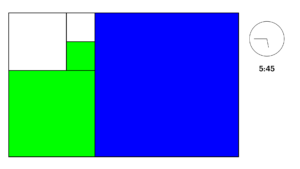
Si el reloj de Fibonacci tuviera esta cara, ¿qué hora indicaría?

Una vez más, las horas se miden sumando los cuadrados rojos y azules. En este caso, como no hay cuadrados pintados de rojo, solamente importan los 5 que indica el azul.

Para los minutos, primero, hay que sumar los verdes y los azules. Azul = 5, Verdes = 3 + 1 = 4. En total, 5+4 = 9.

Pero, para obtener los minutos ¡hay que multiplicar este número por 5! ¿Resultado? 45.

En definitiva, el reloj de Fibonacci en este ejemplo marca las ¡5 y 45!

 

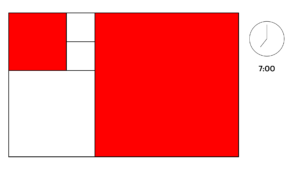
Ejemplo 3

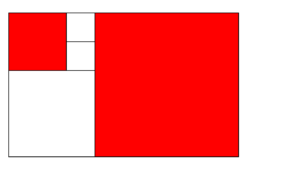
Para determinar las horas, hay que sumar los rojos y azules. Como no hay azules, la hora se calcula sumando los rojos únicamente, es decir: 5+2 = 7

Para determinar los minutos, habría que sumar los verdes y azules. Como no hay de ninguno de los dos colores… ¡no hay minutos!

En definitiva, esa cara del reloj de Fibonacci marcaría la 7.

 

Ejemplo 4

En el siguiente ejemplo, ¿no quiere pensar usted por su cuenta?

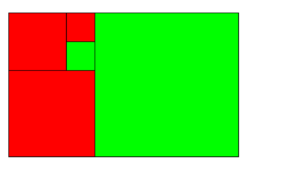
Sigo yo. Para las horas, hay que sumar los rojos y azules. Azules no hay, y rojos están iluminados 3, 2 y 1. En total: 3+2+1 = 6

Para los minutos, hay que sumar los verdes y azules. Azules no hay, y verdes estan iluminados el de 5 y de 1. En total, 5+1 = 6. A este número, hay que multiplicarlo por 5. ¿Resultado? 6 x 5 = 30.

La hora entonces es las 6 y 30.

Un ejemplo más.

Ejemplo 5

 

En este caso, para determinar las horas, hay que sumar el cuadradito de color rojo (1) y el de color azul (5). Como 1+5 = 6 , son seis horas.

Para determinar los minutos, hay que sumar los verdes y azules. Hay uno solo verde (1) y el azul es el mismo (5). En total: 1+5 = 6. Pero como hay que multiplicar por 5, el resultado es 30 minutos. En definitiva, la hora que indica el reloj son las 6 y media otra vez.

Si usted compara los últimos dos ejemplos, verá que la hora que indican es la misma, aunque las luces que están iluminadas son diferentes. Por lo tanto, dada una hora cualquiera, es posible que haya varias maneras de que el reloj las ‘fabrique’. Si le interesa, fíjese qué horas tienen una única forma de ser representadas por el Reloj de Fibonacci (y cuales no).

 

Pregunta final

Para terminar, me imagino que usted se debe estar preguntando: ¿quién —en su sano juicio— habría de hacer este tipo de ejercicio que solo conduce a saber la hora?

 

Respuesta

Posiblemente nadie, sobre todo si está apurado por conocerla. Pero lo que es innegable es que esta idea de Chrétien ([6]) transformó un acto rutinario y aburrido, en excitante y entretenido.

 

Apéndice: La sucesión de Fibonacci

En algún momento, aquí mismo en El Cohete a la Luna voy a tratar de escribir sobre la sucesión de Fibonacci. Por ahora, sólo quiero contar cómo se construye.

Los dos primeros términos son dos números uno. Es decir:

1, 1

A partir de ahora, verá cómo con estos dos números uno se fabrica todos los que siguen.

El tercer número de la sucesión se calcula sumando los dos últimos. Usted debe estar pensando: ¿cómo los dos últimos si solamente tenemos los dos primeros? Es verdad, pero estos dos números uno son los dos primeros pero también los dos últimos.

Como (1+1 = 2), entonces el siguiente número de la sucesión es dos. Ahora tenemos tres números:

1, 1, 2.

Para calcular el que sigue, hago lo mismo, es decir sumo los dos últimos. Como (1+2) = 3, el siguiente término es un tres. Se tiene:

1, 1, 2, 3.

Y así sigo. Una vez más, el próximo aparecerá al sumar los dos últimos, y por lo tanto, será: (2+3) = 5.

1, 1, 2, 3, 5.

Como usted advierte, todo lo que uno tiene que hacer en cada paso, es sumar los dos últimos y seguir indefinidamente.

Los primeros términos son:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ...

y así podría continuar indefinidamente.

Esta sucesión tan inocente aparece en forma visible o intangible en muchísimos lugares de nuestras vidas. En una próxima entrega voy a escribir sobre las apariciones de esta sucesión en lugares inesperados e insólitos. Hay muchísima literatura escrita al respecto, y si le interesa, ponga en cualquier buscador el nombre Fibonacci, y no le alcanzará el tiempo que le queda de vida para leer todo lo que ya hay escrito.

 

 

 

[1] Hay una revista/sitio de internet, “The Fibonacci Quarterly”, que publica únicamente ‘novedades’ que se producen en el mundo y que involucran a la famosa sucesión. Se puede ver acá: http://www.fq.math.ca/

[2] http://basbrun.com/2015/05/04/fibonacci-clock/

[3] Si puede, véalo, porque está muy bien producido.

[4] Por ejemplo, en la hora que transcurre entre las 3 y las 4 de la tarde, solamente habrá estas 12 modificaciones: 3:05 – 3:10 – 3:15 – 3:20 – 3:25 – 3:30 – 3:35 – 3:40 – 3:45 – 3:50 – 3:55 y finalmente, las 4:00

[5] Eso sí: cuando yo escriba que hay que sumar determinado cuadrado, me refiero a que hay que sumar la “longitud” del lado de ese cuadrado.

[6] El ‘verdadero’ reloj de Philippe Chrétien aparece en la Figura 1. Es obvio que mi intención no es ‘vender’ ningún tipo de mercadería, pero la página web en donde figuran todos los datos es esta: https://www.kickstarter.com/projects/basbrun/fibonacci-clock-an-open-source-clock-for-nerds-wit/posts/1229662

 

--------------------------------

Para suscribirte con $ 1000/mes al Cohete hace click aquí

Para suscribirte con $ 2500/mes al Cohete hace click aquí

Para suscribirte con $ 5000/mes al Cohete hace click aquí